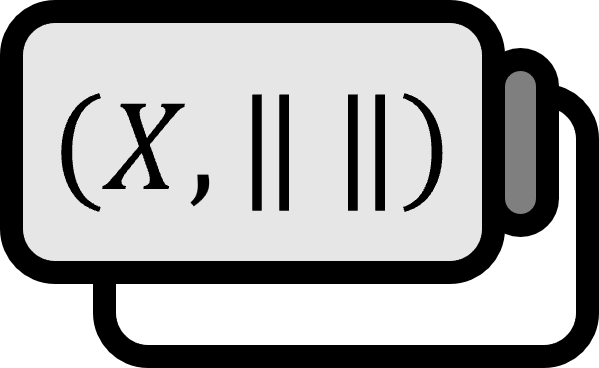
バナッハ空間
定義1
完備なノルム空間をバナッハ空間banach spaceと言う。
説明
完備空間とは、すべてのコーシー列が収束する空間のことを言う。
バナッハ空間は以下の各項をすべて満たす空間として、非常に便利な空間である。距離関数が定義されている上に完備性を備えている。
また、バナッハ空間の例としては、定義域が閉区間である連続関数の集合が考えられる。これは非常に簡単な例でありながら、様々な重要な定理を支えているため、非常に重要な事実でもある。バナッハ空間の例には以下のものがある。
- $C[a,b]$
- $\R^{n}$
- $\mathbb{C}^{n}$
$C[a,b]$に関する証明を紹介する。
証明 1
パート 1. ベクトル空間
閉区間で定義された連続関数は、定数関数 $f(x) = 0$ を単位元として、$f(x) = - f(x)$ を逆元として持つ。また、$C[a,b]$ はスカラーフィールド $\mathbb{R}$上でベクトル空間の条件をよく満たす。
パート 2. ノルム空間
$f \in C [a,b]$ に対して $\| \cdot \|$ を $\displaystyle \| f \| := \sup_{ a \le t \le b } | f (t) |$ として定義すると、ノルムの条件をよく満たす。
パート 3. 完備性
$\left\{ f_{n} \right\}_{n \in \mathbb{N}}$ を $C [a,b]$ のコーシー列としよう。つまり、すべての $\varepsilon / 3 > 0$ に対して、$n,m > N_{1}$ の時いつでも $\| f_{n} (t) - f_{m} (t) \| < \varepsilon / 3$ を満たす $N_{1} \in \mathbb{N}$ が存在する。
$\mathbb{R}$ は完備空間なので、固定された $t_{0} \in [a,b]$ が与えられるたびに、$\displaystyle \lim_{n \to \infty} f_{n} (t_{0})$ はある $f : [a,b] \to \mathbb{R}$ に関して
$$ \lim_{n \to \infty} f_{n} ( t_{0} ) = f ( t_{0} ) $$
と表せる。すると、$f_{n}$ はコーシー列なので、任意の $t \in [a,b]$ に対して、$m \ge N_{2}$ の時に
$$ \begin{align*} | f(t) - f_{m} (t) | =& \left| \lim_{n \to \infty} f_{n} (t) - f_{m} (t) \right| \\ =& \lim_{n \to \infty} | f_{n} (t) - f_{m} (t) | \\ \le & \lim_{n \to \infty} \sup_{t \in [a,b] } | f_{n} (t) - f_{m} (t) | \\ =& \lim_{n \to \infty} \| f_{n} - f_{m} \| \\ <& \varepsilon / 3 \end{align*} $$
を満たす $N_{2}$ が存在する。もちろん、関数 $f$ が連続である保証はまだなく、単にすべての $t \in [a,b]$ に対して最終的に $f_{n} (t)$ に収束する値を関数値として定義されただけである。しかし、この定義から、$f_{n}$ が $f$ に一様収束する、つまりすべての $x,y \in [a,b]$ および $\varepsilon / 3 > 0$ に対して $n \ge N_{3}$ の時に同時に満たされる $N_{3} \in \mathbb{N}$ が存在することを保証することができる。
$$ \left| f_{n} (x) - f(x) \right| < \varepsilon / 3 \\ \left| f_{n} (y) - f(y) \right| < \varepsilon / 3 $$
これで、$f$ が連続関数であることを示すだけである。
空集合でない $E \subset \mathbb{R}$ について、$f : E \to \mathbb{R}$ としよう。
$f$ が連続で、$E$が有界閉区間であれば、$f$ は一様連続である。
$f_{n} : [a,b] \to \mathbb{R}$ は連続であり、$[a,b] \subset \mathbb{R}$ はコンパクトなので、$f_{n}$ は $[a,b]$ で一様連続である。つまり、すべての $x,y \in [a,b]$ および $\varepsilon / 3 > 0$ に対して、$|x-y| < \delta$ の時に満たされる $\delta > 0$ が存在する。
$$ \left| f_{n}(x) - f_{n}(y) \right| < \varepsilon / 3 $$
以上の結果を組み合わせると、$|x-y| < \delta$ および $n \ge N_{3}$ の場合に
$$ \begin{align*} |f(x) - f(y)| \le & \left| f (x) - f_{n} (x) \right| + \left| f_{n}(x) - f_{n}(y) \right| + \left| f_{n} (y) - f(y) \right| \\ =& \varepsilon / 3 + \varepsilon / 3 + \varepsilon / 3 \\ =& \varepsilon \end{align*} $$
を満たす $\delta > 0$ および $N_{3} \in \mathbb{N}$ が存在するため、$f$ は $[a,b]$ で一様連続であり、$f \in C[a,b]$ に収束する。したがって、任意の連続関数のコーシー列 $\left\{ f_{n} \right\}_{n \in \mathbb{N}}$ が一様に何らかの $f \in C[a,b]$ に収束するため、$C[a,b]$ は完備性を有する。
■