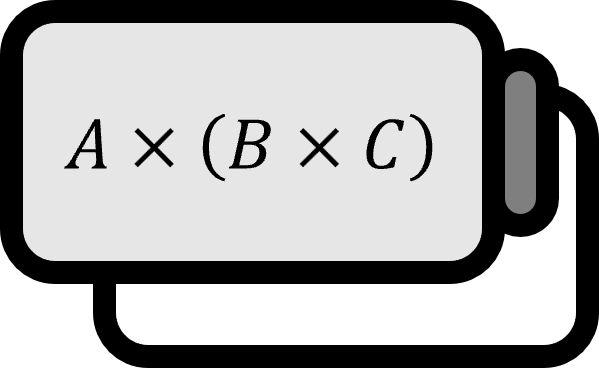3次元デカルト座標系におけるベクトル関数のカール(回転)
定義
ベクトル関数 $\mathbf{F}(x,y,z)=(F_{x},F_{y},F_{z})=F_{x}\hat{\mathbf{x}} + F_{y}\hat{\mathbf{y}} + F_{z}\hat{\mathbf{z}}$に対して、以下のようなベクトルを$\mathbf{F}$のカールcurlと定義し、$\nabla \times \mathbf{F}$と表記する。
$$ \begin{align} \nabla \times \mathbf{F} &= \left( \dfrac{ \partial F_{z}}{ \partial y }-\dfrac{ \partial F_{y}}{ \partial z} \right)\hat{\mathbf{x}}+ \left( \dfrac{ \partial F_{x}}{ \partial z }-\dfrac{ \partial F_{z}}{ \partial x} \right)\hat{\mathbf{y}}+ \left( \dfrac{ \partial F_{y}}{ \partial x }-\dfrac{ \partial F_{x}}{ \partial y} \right)\hat{\mathbf{z}} \label{def1} \\ &=\begin{vmatrix} \hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \\ \dfrac{ \partial }{ \partial x} & \dfrac{ \partial }{ \partial y } & \dfrac{ \partial }{ \partial z} \\ F_{x} & F_{y} &F_{z}\end{vmatrix} \label{def2} \end{align} $$
- $(2)$は$\mathbf{F}$のカールを簡単に覚えるための公式である。行列式と考えてそのまま展開すればよい。
説明
カールは回転と翻訳される。しかし、回転という言葉は日常的すぎる上に、カールではなくrotationと誤解される可能性があるため、생새우초밥집では回転の代わりにカールを使用する。
$\nabla \times \mathbf{F}$は$\mathbf{F}$という物理量がどの方向に回転しているかを教えてくれるベクトルである。$\nabla \times \mathbf{F}$の方向を軸(親指)にして右手の法則を適用すると、右手が包む方向と$\mathbf{F}$が回転する方向が一致する。ベクトル$\nabla \times \mathbf{F}$の大きさは回転の程度を示す。
アインシュタインの表記法とレヴィ-チヴィタ記号を使用すれば、以下のように表すことができる。$\nabla_{j} = \dfrac{\partial }{\partial x_{j}}$と表記するなら、
$$ \nabla \times \mathbf{F} = \epsilon_{ijk}\hat{\mathbf{e}}_{i}\nabla_{j}F_{k} $$
一方、定義で$(1)$という値を$\nabla \times \mathbf{F}$と表記するとしたことに注意しよう。$\nabla$をデル演算子と呼ぶことはあるが、これ自体が何かの意味を持つと考えると、$\nabla \cdot \mathbf{F}$や$\nabla \times \mathbf{F}$を内積や外積と誤解することになりかねない。したがって、$\nabla$は便利な表記法程度にしか理解してはならず、勾配、ダイバージェンス、カールをまとめてデル演算子と呼ぶこともあるし、むしろデル演算子=勾配と考える方が良いかもしれない。詳細は以下で続く。
注意点
$\nabla \times \mathbf{F}$は$\nabla$と$\mathbf{F}$の外積ではない
単に$\nabla \times \mathbf{F}$は$\mathbf{F}$に関する何らかの情報を含むベクトルである。$\nabla$を$\nabla = \dfrac{ \partial }{ \partial x}\hat{\mathbf{x}} + \dfrac{ \partial }{ \partial y}\hat{\mathbf{y}} + \dfrac{ \partial }{ \partial z}\hat{\mathbf{z}}$のようなベクトルと考えて計算すると、結果が$(1)$と完全に一致するため、便宜上$\nabla \times \mathbf{F}$と表記しているだけである。もし$\nabla$を実際のベクトルと仮定すると、おかしな結果になる。
二つのベクトル$\mathbf{A}, \mathbf{B}$に対して次の式が成り立つ。
もし$\nabla$が本当にベクトルだったら、上の公式に代入することができ、次の結果が得られるだろう。
$$ \nabla \times (\nabla \times \mathbf{F})=(\mathbf{F} \cdot \nabla)\nabla - (\nabla \cdot \nabla)\mathbf{F} + \nabla (\nabla \cdot \mathbf{F}) - \mathbf{F} (\nabla \cdot \nabla) $$
しかし、正しい結果は次のようになる。
$$ \nabla \times (\nabla \times \mathbf{F})=\nabla(\nabla \cdot \mathbf{F})-\nabla ^{2} \mathbf{F} $$
他にも例がある。ベクトルの外積は反交換性を持つため、$\nabla \times \mathbf{F}$が外積であるならば、次の式が成り立つはずだ。
$$ \nabla \times \mathbf{F} \overset{?}{=} - \mathbf{F} \times \nabla $$
したがって、$\nabla$はベクトルではなく、$\nabla \times \mathbf{F}$を$\nabla$と$\mathbf{F}$の外積ではないことが分かる。ベクトルではなく、$\nabla \times$自体を一つの関数と考えるべきだ。このように関数を変数とする関数を物理学では演算子と呼ぶ。
では $\nabla \times \mathbf{F}$と$\mathbf{F} \times \nabla$の違いは?
$\nabla \times$はベクトル関数を変数とする、次のように定義される演算子である。
$$ \nabla \times (\mathbf{F}) = \left( \dfrac{ \partial F_{z}}{ \partial y }-\dfrac{ \partial F_{y}}{ \partial z} \right)\hat{\mathbf{x}}+ \left( \dfrac{ \partial F_{x}}{ \partial z }-\dfrac{ \partial F_{z}}{ \partial x} \right)\hat{\mathbf{y}}+ \left( \dfrac{ \partial F_{y}}{ \partial x }-\dfrac{ \partial F_{x}}{ \partial y} \right)\hat{\mathbf{z}} $$
つまり $\nabla \times \mathbf{F}$は $\nabla \times$という演算子(関数)に$\mathbf{F}$という変数を代入したときの関数値である。もちろんこれは再び$(x,y,z)$を変数とするベクトル関数である。$\nabla \times \mathbf{F}$が$\nabla \times$の関数値であるのに対し、$\mathbf{F} \times \nabla$はそれ自体が一つの演算子である。よく使われる数式ではないが、定義するなら次のような微分演算子であると言える。
$$ \begin{align*} \mathbf{F} \times \nabla &= \begin{vmatrix} \hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \\ F_{x} & F_{y} &F_{z} \\ \dfrac{ \partial }{ \partial x} & \dfrac{ \partial }{ \partial y } & \dfrac{ \partial }{ \partial z} \end{vmatrix} \\ &= \left( F_{y}\dfrac{ \partial }{ \partial z} - F_{z}\dfrac{ \partial }{ \partial y} \right)\hat{\mathbf{x}} + \left( F_{z}\dfrac{ \partial }{ \partial x} - F_{x}\dfrac{ \partial }{ \partial z} \right)\hat{\mathbf{y}} + \left( F_{x}\dfrac{ \partial }{ \partial y} - F_{y}\dfrac{ \partial }{ \partial x} \right)\hat{\mathbf{z}} \end{align*} $$
導出
ここで、ベクトル関数が回転する方向(時計回りか反時計回りか)を示す関数について考えてみましょう。重要なのは、回転面内のどの方向も回転の方向を特定できないということです。下の図を見てください。

- ベクトル $-\hat{\mathbf{x}}$は点 $A$での動きは説明できますが、$B$での動きは説明できません。
- ベクトル $\hat{\mathbf{y}}$は点 $C$での動きは説明できますが、$D$での動きは説明できません。
- ベクトル $\hat{\mathbf{x}} + \hat{\mathbf{y}}$は経路 $F$を説明できますが、$G$を説明できません。
これは時計回りの場合にも同じです。回転方向を特定するためには回転面を離れる必要があることが理解できるでしょう。実際、これを決定するための良い方法が既にあります。それは、右手の法則を使うことです。右手が巻き込む方向の回転軸を親指の方向として決定します。したがって、$xy$平面で反時計回りに回る回転の軸(方向)は$\hat{\mathbf{z}}$であり、時計回りに回る回転の軸(方向)は$-\hat{\mathbf{z}}$です。
それでは、$\mathbf{F}$が$xy$平面で反時計回りに回っている場合、$\hat{\mathbf{z}}$方向を示す値、つまり正の値を見つけてみましょう。回転は簡単に以下のように四角形で表現しましょう。
経路①は点 $a$から点 $b$まで動き、$\mathbf{F}(a) = (1,0,0)$, $\mathbf{F}(b) = (0,1,0)$としましょう。すると、点 $a$から点 $b$まで$x$は$+1$だけ変化し、$F_{y}$も$+1$だけ変化するので、次のようになります。
$$ \dfrac{\partial F_{y}}{\partial x} \gt 0 $$
同様に、点 $b$から点 $c$までの経路で、$y$は$+1$だけ変化し、$F_{x}$は$-1$だけ変化します。4つの経路すべてを確認すると、
$$ \dfrac{\partial F_{y}}{\partial x} \gt 0 \quad \text{in path $\textcircled{1}$, $\textcircled{3}$} $$
$$ \dfrac{\partial F_{x}}{\partial y} \lt 0 \quad \text{in path $\textcircled{2}$, $\textcircled{4}$} $$
したがって、上記のように反時計回りに回転するベクトル $\mathbf{F}$に対して、以下の値は常に正です。
$$ \dfrac{\partial F_{y}}{\partial x} - \dfrac{\partial F_{x}}{\partial y} \gt 0 $$
逆に、$\mathbf{F}$が時計回りに回転している場合、上記の値は常に負です。それでは、ベクトル関数 $\mathbf{F}$を代入すると、$xy$平面で回転する方向と大きさを示す演算子 $\operatorname{curl}_{xy}$を次のように定義できます。
$$ \operatorname{curl}_{xy} (\mathbf{F}) = \left( \dfrac{\partial F_{y}}{\partial x} - \dfrac{\partial F_{x}}{\partial y} \right) \hat{\mathbf{z}} $$
- この関数の $\hat{\mathbf{z}}$ 成分の符号は、$\mathbf{F}$が$xy$平面で回転する方向を示す。
- $+$の場合、$\mathbf{F}$は$xy$平面で反時計回りに回転する。
- $-$の場合、$\mathbf{F}$は$xy$平面で時計回りに回転する。
- $0$の場合、回転しない。
- この関数の $\hat{\mathbf{z}}$ 成分の大きさは、$\mathbf{F}$が$xy$平面でどれだけ速く回転しているかを示す。
このような議論を$yz$平面と$zx$平面にも適用することで、$\mathbf{F}$が3次元空間で回転している方向と大きさを示すベクトル$\nabla \times \mathbf{F}$を次のように定義することができます。
$$ \nabla \times \mathbf{F} := \left( \dfrac{\partial F_{z}}{\partial y} - \dfrac{\partial F_{y}}{\partial z} \right)\hat{\mathbf{x}} + \left( \dfrac{\partial F_{x}}{\partial z} - \dfrac{\partial F_{z}}{\partial x} \right)\hat{\mathbf{y}} + \left( \dfrac{\partial F_{y}}{\partial x} - \dfrac{\partial F_{x}}{\partial y} \right)\hat{\mathbf{z}} $$
■
関連する公式
リニアリティ: $$ \nabla \times (\mathbf{A} + \mathbf{B}) = \nabla \times \mathbf{A} + \nabla \times \mathbf{B} $$
$$ \nabla \times (f\mathbf{A}) = f(\nabla \times \mathbf{A}) - \mathbf{A} \times (\nabla f) $$
$$ \nabla \times (\mathbf{A} \times \mathbf{B}) = (\mathbf{B} \cdot \nabla)\mathbf{A} - (\mathbf{A} \cdot \nabla)\mathbf{B} + \mathbf{A} (\nabla \cdot \mathbf{B}) - \mathbf{B} (\nabla \cdot \mathbf{A}) $$
$$ \nabla \times (\nabla f) = \mathbf{0} $$
$$ \nabla \times (\nabla \times \mathbf{F}) = \nabla (\nabla \cdot \mathbf{F}) - \nabla^{2} \mathbf{F} $$
ストークスまとめ $$ \int_{\mathcal{S}} (\nabla \times \mathbf{v} )\cdot d\mathbf{a} = \oint_{\mathcal{P}} \mathbf{v} \cdot d\mathbf{l} $$
積分式 $$ \int_{\mathcal{V}} (\nabla \times \mathbf{v}) d \tau = - \oint_{\mathcal{S}} \mathbf{v} \times d \mathbf{a} $$
$$ \int_{\mathcal{S}} \nabla T \times d \mathbf{a} = - \oint_{\mathcal{P}} T d \mathbf{l} $$
部分積分 $$ \int_{\mathcal{S}} f \left( \nabla \times \mathbf{A} \right)\mathbf{A} \cdot d \mathbf{a} = \int_{\mathcal{S}} \left[ \mathbf{A} \times \left( \nabla f \right) \right] \cdot d\mathbf{a} + \oint_{\mathcal{P}} f\mathbf{A} \cdot d\mathbf{l} $$
$$ \int_{\mathcal{V}} \mathbf{B} \cdot \left( \nabla \times \mathbf{A} \right) d\tau = \int_{\mathcal{V}} \mathbf{A} \cdot \left( \nabla \times \mathbf{B} \right) d\tau + \oint_{\mathcal{S}} \left( \mathbf{A} \times \mathbf{B} \right) \cdot d \mathbf{a} $$
証明
線形性
アインシュタイン表記法, レヴィ・チビタ記号を使います。$\nabla_{j} = \dfrac{\partial }{\partial x_{j}}$ とすると、
$$ \begin{align*} \left[ \nabla \times (\mathbf{A} + \mathbf{B}) \right]_{i} &= \epsilon_{ijk} \nabla_{j} (\mathbf{A} + \mathbf{B})_{k} \\ &= \epsilon_{ijk} \nabla_{j} (A_{k} + B_{k}) \\ &= \epsilon_{ijk} \nabla_{j}A_{k} + \epsilon_{ijk} \nabla_{j}B_{k} \\ &= [\nabla \times \mathbf{A}]_{i} + [\nabla \times \mathbf{B}]_{i} \\ \end{align*} $$
第三の等号は、$\dfrac{\partial (A_{k} + B_{k})}{\partial x_{j}} = \dfrac{\partial A_{k}}{\partial x_{j}} + \dfrac{\partial B_{k}}{\partial x_{j}}$であるため成立します。
■