📂バナッハ空間

有限次元ベクトル空間上で定義された全てのノルムは同値であることの証明

定理 ¹

有限次元ベクトル空間上で定義されるすべてのノルムは等価である。

説明

ユークリッド空間で定義されるすべてのノルムが等価であるという事実は、この定理の系である。

証明

戦略: $c \| v \| _{\alpha} \le \| v \| _{\beta} \le C \| v \| _{\alpha}$ を満たす $c , C >0$ が存在することを示せば、二つのノルム $\left\| \cdot \right\|_{\alpha}$ と $\left\| \cdot \right\|_{\beta}$ は等価である。最大最小値定理を通じて $\displaystyle { { \| v \| _{\beta} } \over {\| v \| _{\alpha} } }$ の最大値と最小値の存在を一度に示す。

---

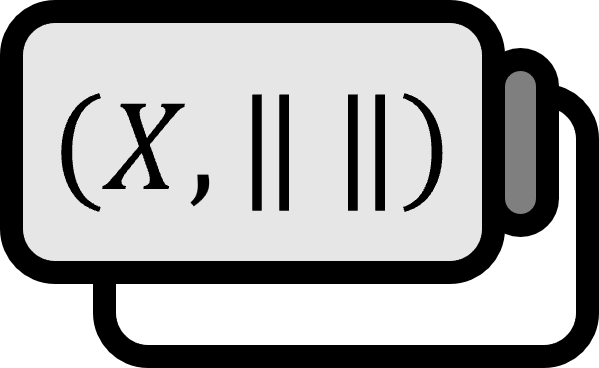
有限次元ベクトル空間 $X$ でノルムが定義されている場合、基底 $\left\{ e_{1} , \cdots , e_{n} \right\}$ が存在する。したがって、$X$ のすべてのベクトルは $(\lambda_{1} , \cdots , \lambda_{n} ) = \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n}$ のように表される。$X$ で定義された三つのノルム、$\left\| \cdot \right\|_{1}$、$\left\| \cdot \right\|_{2}$、そして $\left\| \cdot \right\|$ を考える。特に $\left\| \cdot \right\|$ は

$$ \| \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \| : = \sum_{k=1}^{n} | \lambda_{k} | $$

線形結合の係数の絶対値をすべて足し上げるノルムとして定義される。今、$\left\| \cdot \right\|_{1} \sim \left\| \cdot \right\|$ と $\left\| \cdot \right\| \sim \left\| \cdot \right\|_{2}$ を示せば、等価関係の推移性により任意の二つのノルムは $\left\| \cdot \right\|_{1} \sim \left\| \cdot \right\|_{2}$ を満たす。

• パート1.

  関数 $f : ( \mathbb{C}^{n} , \left\| \cdot \right\| ) \to \mathbb{R}$ を $f( \lambda_{1} , \cdots , \lambda_{n} ) = \| \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \|_{1}$ として定義しよう。そして、それぞれが $\lambda_{1} , \cdots , \lambda_{n}$ に収束する数列 $\left\{ \lambda_{1}^{(j)} \right\}_{j \in \mathbb{N} } , \cdots , \left\{ \lambda_{n}^{(j)} \right\}_{j \in \mathbb{N} }$ を定義しよう。

  $$ \begin{align*} & \left| f( \lambda_{1}^{(j)} , \cdots , \lambda_{n}^{(j)} ) - f( \lambda_{1} , \cdots , \lambda_{n} ) \right| \\ =& \left| \| \lambda_{1}^{(j)} e_{1} + \cdots + \lambda_{n}^{(j)} e_{n} \|_{1} - \| \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \|_{1} \right| \\ \le & \left\| \left( \lambda_{1}^{(j)} e_{1} + \cdots + \lambda_{n}^{(j)} e_{n} \right) - \left( \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \right) \right\|_{1} \\ \le & \sum_{k=1}^{n} \left\| \left( \lambda_{k}^{(j)} e_{k} - \lambda_{k} e_{k} \right) \right\|_{1} \\ \le & \sum_{k=1}^{n} \left| \lambda_{k}^{(j)}- \lambda_{k} \right| \max_{1 \le k \le n} \left\| e_{k} \right\|_{1} \end{align*} $$

  すなわち、$j \to \infty$ の時、$\left| f( \lambda_{1}^{(j)} , \cdots , \lambda_{n}^{(j)} ) - f( \lambda_{1} , \cdots , \lambda_{n} ) \right| \to 0$ だから、$f$は連続関数だ。

• パート2.

  $X$ で係数の絶対値の合計が $1$ であるベクトルだけを集めた集合

  $$ S := \left\{ \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \ : \ \sum_{k=1}^{n} | \lambda_{k}|=1, \lambda_{k} \in \mathbb{C} \right\} $$

  はコンパクトであり、$f$ は連続であるから、最大最小値定理により

  $$ f(S) = \left\{ \| \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \|_{1} \ : \ \sum_{k=1}^{n} | \lambda_{k}|=1, \lambda_{k} \in \mathbb{C} \right\} $$

  は最小値 $m$ と最大値 $M$ を持つ。したがって、

  $$ m \le \| \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \|_{1} \le M $$

• パート3.

  $\displaystyle \sum_{k=1}^{n} | \alpha_{k}| \ne 1$ である $( \alpha_{1} e_{1} + \cdots + \alpha_{n} e_{n} ) \in X$ に対して

  $$ m \le \left\| {{\alpha_{1} } \over { \sum_{k=1}^{n} | \alpha_{k}|}} e_{1} + \cdots + {{\alpha_{n}} \over { \sum_{k=1}^{n} | \alpha_{k}|}} e_{n} \right\|_{1} \le M $$

  ノルムの性質により

  $$ m \le {{1} \over {\sum_{k=1}^{n} | \alpha_{k}|}} \| \alpha_{1} e_{1} + \cdots + \alpha_{n} e_{n} \|_{1} \le M $$

  $\displaystyle \sum_{k=1}^{n} | \alpha_{k} | = \| \alpha_{1} e_{1} + \cdots + \alpha_{n} e_{n} \|$ だから

  $$ m \| \alpha_{1} e_{1} + \cdots + \alpha_{n} e_{n} \| \le \| \alpha_{1} e_{1} + \cdots + \alpha_{n} e_{n} \|_{1} \le M \| \alpha_{1} e_{1} + \cdots + \alpha_{n} e_{n} \| $$

  したがって、ノルムの等価関係が定義されているとおりに

  $$ \left\| \cdot \right\| \sim \left\| \cdot \right\|_{1} $$

• パート4.

  同じ方法で $\left\| \cdot \right\| \sim \left\| \cdot \right\|_{2}$ が示されれば、等価関係の推移性により

  $$ \left\| \cdot \right\|_{1} \sim \left\| \cdot \right\|_{2} $$

■