実数、複素数、セミノルムに対するハーン・バナッハの定理
実数に関するハーン・バナッハの定理1
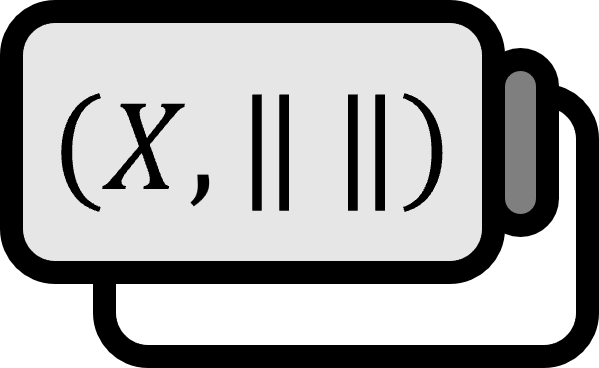
$X$は$\mathbb{R}$-ベクトル空間であり、$Y \subset X$とする。$p : X \to \mathbb{ R}$を$X$の準線形 線形汎関数とする。今、$y^{\ast} : Y \to \mathbb{ R}$が以下の条件を満たす$Y$の$\mathbb{R}$-線形汎関数であると仮定する。
$$ y^{\ast}(y) \le p(y)\quad \forall y\in Y $$
すると、以下の条件を満たす$X$の線形汎関数$x^{\ast} : X \to \mathbb{R}$が存在する。
(a) $x^{\ast}(y)=y^{\ast}(y),\quad \forall y \in Y$
(b) $x^{\ast}(x) \le p(x),\quad \forall x \in X$
説明
$\mathbb{R}-$ベクトル空間とは、体$\mathbb{R}$に関するベクトル空間のことである。つまり、ベクトル空間のスカラー倍に関する条件$(M1)$〜$(M5)$が実数に対して成立するという意味である。同様に、$\mathbb{R}$-線形とは、線形の二つの性質のうちスカラー倍に関する内容が実数に対して成立するという意味である。
$X, Y$が$\mathbb{R}$-ベクトル空間であるため、$y^{\ast}$、$x^{\ast}$が線形であることと$\mathbb{R}$-線形であることは同じ意味である。この部分が混乱する場合は、**$\mathbb{R}$-、$\mathbb{C}$-はこの記事では存在しない文字と考えても、証明を理解する上で問題はない。**後にハーン・バナッハの定理をノルム空間に適用する際には、関数$p$がノルムに対応する。この定理の証明は省略し、複素数に関するハーン・バナッハの定理の証明に使用する補助定理として利用する。
複素数に関するハーン・バナッハの定理2
$X$は$\mathbb{C}$-ベクトル空間であり、$Y \subset X$とする。$p : X \to \mathbb{ R}$を以下のように定義された準線形汎関数とする。
$$ p(\lambda x)=|\lambda| p(x),\quad x\in X, \lambda \in \mathbb{C} $$
そして、$y^{\ast} : Y \to \mathbb{ C}$が以下の条件を満たす$Y$の線形汎関数であると仮定する。
$$ \begin{equation} \text{Re}\left( y^{\ast}(y) \right) \le p(y),\quad \forall y\in Y \end{equation} $$
すると、以下の条件を満たす$X$の線形汎関数$x^{\ast} : X \to \mathbb{C}$が存在する。
- $x^{\ast}(y)=y^{\ast}(y),\quad \forall y \in Y$
- $\text{Re}(x^{\ast}(x)) \le p(x),\quad \forall x \in X$
説明
実数に関する定理と比較した場合、$p$の値域が$\mathbb{R}$であることは変わらないが、これは上述のように$X$がノルム空間の場合、$p$がノルムに対応するからである。$X$、$Y$は$\mathbb{C}$-ベクトル空間であり、$\mathbb{R} \subset \mathbb{C}$であるため、$\mathbb{R}$-ベクトル空間である条件も満たされる。すべての複素数に対してベクトル空間の条件$(M1)$〜$(M5)$が成立する場合、自動的にすべての実数に対しても成立するからである。同様に、$y^{\ast}$、$x^{\ast}$は$\mathbb{C}$-線形であるため、$\mathbb{R}-$線形である条件も満たされる。
証明
関数$\psi : Y \to \mathbb{ R}$を以下のように定義する。
$$ \psi (y) = \text{Re} ( y^{\ast}(y) ) $$
すると、$\psi$も$Y$の$\mathbb{C}$-線形汎関数であることが示される。これは$\mathrm{ Re}$と$y^{\ast}$が線形であるために自明な結果であり、示す過程は非常に簡単なので省略する。$\psi$の定義と$(1)$により、以下の式が成立する。
$$ \psi(y)= \text{Re} \left( y^{\ast}(y) \right) \le |y^{\ast}(y)| \le p(y) $$
すると、実数に関するハーン・バナッハの定理により、以下の条件を満たす$X$の$\mathbb{R}$-線形汎関数$\Psi : X \to \mathbb{ R}$が存在する。
$$ \Psi (y) = \psi (y),\quad \forall y \in Y $$
$$ \Psi (x) \le p(x),\quad \forall x \in X $$
そして、新たに関数$\Phi : X \to \mathbb{ C}$を以下のように定義しよう。最終的な目標は、以下のように定義された$\Phi$が、定理で存在すると言われていた$x^{\ast}$であることを示すことである。
$$ \Phi (x) := \Psi (x) -i \Psi(ix) $$
すると、$\Phi$が$X$の線形汎関数であることが確認できる。$\Psi$が$\mathbb{R}$-線形であるため、加法と実数乗に関しては線形性が自明であるため、$\Phi(ix)=i\Phi(x)$のみを確認すればよい。
$$ \begin{align*} \Phi(ix) =&\ \Psi(ix) -i \Psi( -x) \\ =&\ \Psi(ix)+i\Psi(x) \\ =&\ -i^2 \Psi(ix)+i\Psi(x) \\ =&\ i \big( \Psi(x)-i\Psi(ix) \big) \\ =&\ i\Phi(x) \end{align*} $$
$\Phi$が**(a)**を満たすことは、以下のように示すことができる。$y \in Y$とすると、
$$ \begin{align*} \Phi(y) =&\ \Psi (y) -i \Psi(iy) \\ =&\ \psi(y) -i\psi(iy) \\ =&\ \text{Re} \left( y^{\ast}(y) \right)-i\text{Re} \left( y^{\ast}(iy) \right) \\ =&\ \text{Re} \left( y^{\ast}(y) \right) +\text{Im} \left(-iy^{\ast}(iy) \right) \\ =&\ \text{Re} \left( y^{\ast}(y) \right) +\text{Im} \left( y^{\ast}(y) \right) \\ =&\ y^{\ast}(y) \end{align*} $$
$\Phi$が**(b)**を満たすことを示すのはさらに簡単である。
$$ \mathrm{Re }\left( \Phi(x) \right) = \Psi(x) \le p(x) $$
したがって、$\Phi$が$X$の線形汎関数であり、**(a), (b)**を満たすため、$x^{\ast}=\Phi$が存在する。
■
セミノルムに関するハーン・バナッハの定理
$X$は$\mathbb{C}$-ベクトル空間であり、$Y \subset X$とする。$p : X \to \mathbb{ R}$を$X$のセミノルムとする。そして、$y^{\ast} : Y \to \mathbb{ C}$が以下の条件を満たす$Y$の線形汎関数であると仮定する。
$$ | y^{\ast}(y) | \le p(y),\quad \forall y\in Y $$
すると、以下の条件を満たす$X$の線形汎関数$x^{\ast} : X \to \mathbb{C}$が存在する。
$x^{\ast}(y)=y^{\ast}(y),\quad \forall y \in Y$
$| x^{\ast}(x) | \le p(x),\quad \forall x \in X$
証明
セミノルムと準線形の定義から、$p$がセミノルムであれば準線形の条件も自動的に満たされる。
まず、以下の式が成立することは自明である
$$ \text{Re} \left( y^{\ast}(y) \right) \le |y^{\ast}(y) | \le p(y) $$
したがって、複素数に関するハーン・バナッハの定理により、以下の二つの条件を満たす$X$の線形汎関数$x^{\ast} : X \to \mathbb{C}$が存在する。
$$ x^{\ast}(y)=y^{\ast}(y) \quad \forall y \in Y $$
$$ \text{Re} \left( x^{\ast}(x) \right) \le p(x) \quad \forall x \in X $$
$S = \left\{ \lambda \in \mathbb{C} : | \lambda | =1 \right\}$とする。すると、
$$ \begin{align*} \text{Re} \left( \lambda x^{\ast}(x) \right) =&\ \text{Re} \left( \lambda x^{\ast}(\lambda x) \right) \\ \le & p(\lambda x) \\ =&\ |\lambda| p(x)=p(x) \quad \forall x \in X \end{align*} $$
この時、固定された$x \in X$に対して$|x^{\ast}(x)|=\lambda x^{\ast}(x)$を満たす$\lambda \in S$を常に見つけることができる。したがって、$x$とその特定の$\lambda$に対して、以下の式が成立する。
$$ | x^{\ast}(x) | =\lambda x^{\ast}(x) = \text{Re} \left( \lambda x^{\ast}(x) \right) \le p(x), \quad \forall x \in X $$
$X$の線形汎関수$x^{\ast}$が二つの条件を満たすため、証明完了。
■
付録
固定された$x$に対して$x^{\ast}(x)=a+ib$とする。$\lambda=c+id$とする。$\lambda$の条件により$c^2+d^2 =1$であるため、$\lambda=c+i\sqrt{1-c^2}$である。また、$|x^{\ast}(x)|=\sqrt{a^2+b^2}$である。$\lambda x^{\ast}(x)=(ac-b\sqrt{1-c^2})+i(a\sqrt{1-c^2}+bc)$であり、$|x^{\ast}(x)|$が非負の実数であるため、
$$ \begin{align*} && a\sqrt{1-c^2}+bc =&\ 0 \\ \implies&& a^2(1-c^2) =&\ b^2c^2 \\ \implies&& a^2 =&\ (a^2+b^2)c^2 \\ \implies&& c^2 =&\ \dfrac{a^2}{a^2+b^2} \tag{2} \end{align*} $$
便宜上$c=\dfrac{a}{\sqrt{a^2+b^2}}$とし、$d=\dfrac{-b}{\sqrt{a^2+b^2}}$とする。すると、$(2)$と$c^2+d^2=1$が成立する。また、$|x^{\ast}(x)|=ac-bd=\sqrt{a^2+b^2}$が成立する。したがって、固定された$x$に対して$x^{\ast}(x)=a+ib$であれば、$\lambda=\dfrac{a}{\sqrt{a^2+b^2}}-i\dfrac{b}{\sqrt{a^2+b^2}}\in S$に対して$|x^{\ast}(x)|=\lambda x^{\ast}(x)$が成立する。