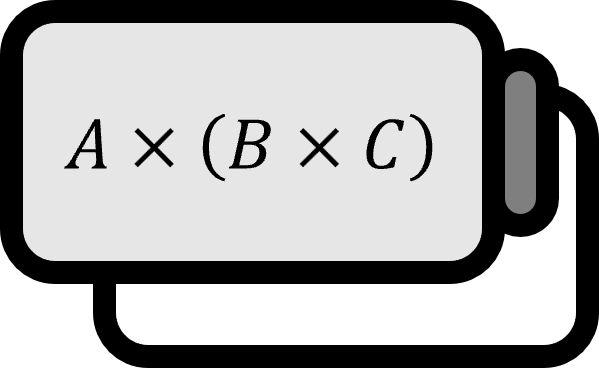📂数理物理学

レヴィ-チヴィタ記号

定義

以下のように定義される$\epsilon_{ijk}$を レビ-チビタ記号^{Levi-Civita-symbol} という。

$$\epsilon_{ijk} = \begin{cases} +1 & \text{if} \ \epsilon_{123}, \epsilon_{231}, \epsilon_{312} \\ -1 & \text{if} \ \epsilon_{132}, \epsilon_{213}, \epsilon_{321} \\ 0 & \text{if} \ i=j \ \text{or} \ j=k \ \text{or} \ k=i \end{cases}$$

説明

クロネッカーのデルタがインデックス同士が同じかだけを考えたとするなら、レビ-チビタ記号は定義から見えるようにインデックスの順番も値に影響を与える。$\epsilon_{ijk}$は$i$、$j$、$k$が重複なしで昇順$(1\to 2\to 3\to 1)$であれば$+1$、重複なしで降順$(3\to 2\to 1\to 3)$であれば$-1$、一つでも重複があれば$0$を値とする。単純に述べれば上のようで、全部の値を列挙すれば合計$3\times 3\times 3=27$個で、その中で$0$ではないのは$6$個である。

$$\begin{array}{|c|c|c|c|}\hline i=1 & k=1 & k=2 & k=3 \\ \hline j=1 & \epsilon_{111}=0 & \epsilon_{112}=0 & \epsilon_{113}=0 \\ j=2 & \epsilon_{121}=0 & \epsilon_{122}=0 & \epsilon_{123}=1 \\ j=3 & \epsilon_{131}=0 & \epsilon_{132}=-1 & \epsilon_{133}=0 \\ \hline \end{array}\quad \begin{array}{|c|c|c|c|}\hline i=2 & k=1 & k=2 & k=3 \\ \hline j=1 & \epsilon_{211}=0 & \epsilon_{212}=0 & \epsilon_{213}=-1 \\ j=2 & \epsilon_{221}=0 & \epsilon_{222}=0 & \epsilon_{223}=0 \\ j=3 & \epsilon_{231}=1 & \epsilon_{232}=0 & \epsilon_{233}=0 \\ \hline \end{array} \\ {} \\ \begin{array}{|c|c|c|c|}\hline i=3 & k=1 & k=2 & k=3 \\ \hline j=1 & \epsilon_{311}=0 & \epsilon_{312}=1 & \epsilon_{313}=0 \\ j=2 & \epsilon_{321}=-1 & \epsilon_{322}=0 & \epsilon_{323}=0 \\ j=3 & \epsilon_{331}=0 & \epsilon_{332}=0 & \epsilon_{333}=0 \\ \hline \end{array}$$

$3$次テンソルの一例である。

例

外積

レビ-チビタ記号を使うと、二つのベクトルの外積を非常に簡単に表現できる。3次元直交座標系で二つのベクトルの外積は以下の通りである。

$$\begin{align*} \mathbf{A} \times \mathbf{B} =&\ \hat{\mathbf{e}}_{x} (A_{y}B_{z}-A_{z}B_{y}) + \hat{\mathbf{e}}_{y} (A_{z}B_{x}-A_{x}B_{z}) + \hat{\mathbf{e}}_{z} (A_{x}B_{y}-A_{y}B_{x}) \\ =&\ \begin{vmatrix} \hat{\mathbf{e}}_{x} \quad \hat{\mathbf{e}}_{y} \quad \hat{\mathbf{e}}_{z} \\ A_{x} \quad A_{y} \quad A_{z} \\ B_{x} \quad B_{y} \quad B_{z} \end{vmatrix} \end{align*}$$

ここで$x=1$、$y=2$、$z=3$とすると、二つのベクトルの外積はレビ-チビタ記号を使用して以下のように表現できる。

$$\sum\limits_{i=1}^{3} \sum\limits_{j=1}^{3} \sum\limits_{k=1}^{3} {\epsilon_{ijk} \hat{\mathbf{e}}_{i} A_{j}B_{k}}$$

$0$ではない項だけを展開すると、以下のようになる。

$$\begin{align*} & \sum\limits_{i=1}^{3} \sum\limits_{j=1}^{3} \sum\limits_{k=1}^{3} {\epsilon_{ijk} \hat{\mathbf{e}}_{i} A_{j}B_{k}} \\ =&\ \epsilon_{123} \hat{\mathbf{e}}_{1}A_{2}B_{3} + \epsilon_{132} \hat{\mathbf{e}}_{1}A_{3}B_{2} + \epsilon_{ 231 }\hat{\mathbf{e}}_{2}A_{3}B_{1} + \epsilon_{213}\hat{\mathbf{e}}_{2}A_{1}B_{3} + \epsilon_{312}\hat{\mathbf{e}}_{3}A_{1}B_{2} + \epsilon_{321}\hat{\mathbf{e}}_{3}A_{2}B_{1} \end{align*}$$

ここで$\epsilon_{123}=\epsilon_{231}=\epsilon_{312}=1$、$\epsilon_{132}=\epsilon_{213}=\epsilon_{321}=-1$を代入して整理すると、以下のようになる。

$$\begin{align*} & \sum\limits_{i=1}^{3} \sum\limits_{j=1}^{3} \sum\limits_{k=1}^{3} {\epsilon_{ijk} A_{i}B_{j}}\hat{\mathbf{e}}_{k} \\ =&\ \hat{\mathbf{e}}_{1}\left( A_{2}B_{3} - A_{3}B_{2} \right) + \hat{\mathbf{e}}_{2}\left( A_{3}B_{1} - A_{1}B_{3} \right) + \hat{\mathbf{e}}_{3}\left( A_{1}B_{2} - A_{2}B_{1} \right) \end{align*}$$

最後に$1$、$2$、$3$にそれぞれ$x$、$y$、$z$を代入すると、以下を得る。

$$\hat{\mathbf{e}}_{x}\left( A_{y}B_{z} - A_{z}B_{y} \right) + \hat{\mathbf{e}}_{y}\left( A_{z}B_{x} - A_{x}B_{z} \right) + \hat{\mathbf{e}}_{z}\left( A_{x}B_{y} - A_{y}B_{x} \right)$$

したがって、以下の結果を得る。

$$\mathbf{A} \times \mathbf{ B } = \sum \limits_{i=1}^{3} \sum \limits_{j=1}^{3} \sum \limits_{k=1}^{3} \epsilon_{ijk}\hat{\mathbf{e}}_{i}A_{j}B_{k}$$

アインシュタインの記法を使えば、以下のようになる。

$$\mathbf{A} \times \mathbf{ B } = \epsilon_{ijk}\hat{\mathbf{e}}_{i}A_{j}B_{k}$$

外積の各成分も容易に表現できるが、上の式から分かるように、$(\mathbf{A} \times \mathbf{B})$の$i$成分は以下の通りである。

$$(\mathbf{A} \times \mathbf {B})_{i}=\epsilon_{ijk}A_{j}B_{k}$$

行列式

$3 \times 3$行列$A = [a_{ij}]$の行列式は、以下のように表される。

$$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{vmatrix} = \sum\limits_{i,j,k=1}^{3} \epsilon_{ijk}a_{1i}a_{2j}a_{3k}$$

示す方法は簡単だ。行列式を展開し、行列の各成分の二番目のインデックスをよく見ると、インデックスのレビ-チビタ記号が各項の符号と一致することがわかる。

$$\begin{align*} & \det A \\ &= a_{11}(a_{22}a_{33} - a_{23}a_{32}) + a_{12}(a_{23}a_{31} - a_{21}a_{33}) + a_{13}(a_{21}a_{32} - a_{22}a_{31}) \\ &= a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} + a_{12}a_{23}a_{31} - a_{12}a_{21}a_{33} + a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} \\ &= a_{1\textcolor{red}{1}}a_{2\textcolor{red}{2}}a_{3\textcolor{red}{3}} - a_{1\textcolor{red}{1}}a_{2\textcolor{red}{3}}a_{3\textcolor{red}{2}} + a_{1\textcolor{red}{2}}a_{2\textcolor{red}{3}}a_{3\textcolor{red}{1}} - a_{1\textcolor{red}{2}}a_{2\textcolor{red}{1}}a_{3\textcolor{red}{3}} + a_{1\textcolor{red}{3}}a_{2\textcolor{red}{1}}a_{3\textcolor{red}{2}} - a_{1\textcolor{red}{3}}a_{2\textcolor{red}{2}}a_{3\textcolor{red}{1}} \\ &= \epsilon_{\textcolor{red}{123}}a_{1\textcolor{red}{1}}a_{2\textcolor{red}{2}}a_{3\textcolor{red}{3}} + \epsilon_{\textcolor{red}{132}}a_{1\textcolor{red}{1}}a_{2\textcolor{red}{3}}a_{3\textcolor{red}{2}} + \epsilon_{\textcolor{red}{231}}a_{1\textcolor{red}{2}}a_{2\textcolor{red}{3}}a_{3\textcolor{red}{1}} + \epsilon_{\textcolor{red}{213}}a_{1\textcolor{red}{2}}a_{2\textcolor{red}{1}}a_{3\textcolor{red}{3}} + \epsilon_{\textcolor{red}{312}}a_{1\textcolor{red}{3}}a_{2\textcolor{red}{1}}a_{3\textcolor{red}{2}} + \epsilon_{\textcolor{red}{321}}a_{1\textcolor{red}{3}}a_{2\textcolor{red}{2}}a_{3\textcolor{red}{1}} \\ &= \sum\limits_{i,j,k=1}^{3} \epsilon_{ijk}a_{1i}a_{2j}a_{3k} \end{align*}$$

公式

(a) 一つのインデックスが同じ場合: $\epsilon_{ijk}\epsilon_{lmk}=\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl}$

(b) 二つのインデックスが同じ場合: $\epsilon_{ijk}\epsilon_{ljk}=2\delta_{il}$

(c) 三つのインデックスが同じ場合: $\epsilon_{ijk}\epsilon_{ijk}=6$