측도의 일반적인 정의
정의
가측 공간 $(X,\mathcal{E})$가 주어졌다고 하자. 아래의 세 조건을 만족하는 확장된 실수값을 갖는 함수 $\mu : \mathcal{E} \to \overline{\mathbb{R}}$를 측도measure 라고 한다.
(a) $\mu ( \varnothing ) = 0$
(b) $\mu (E) \ge 0,\quad \forall E\in \mathcal{E}$
(c) $\left\{E_{j}\right\}$를 $\mathcal{E}$에서 서로소인 집합들의 수열이라고 하자. 그러면 다음을 만족한다.
$$ \mu \left( \bigcup _{j=1}^\infty E_{j} \right) =\sum \limits_{j=1}^\infty \mu (E_{j}) $$
순서쌍 $(X,\mathcal{E}, \mu)$를 측도 공간measure space 이라 한다.
두 집합 $E_{1}$, $E_2$가 $E_{1} \cap E_2=\varnothing$를 만족하면 $E_{1}$와 $E_2$를 서로소disjoint인 집합이라 한다.
설명
$\mu$의 조건을 $\mu\ :\ \mathcal{E} \rightarrow [0,\infty]$로 바꾸면 (b) 를 포함하므로 생략할 수 있다.
조건 (c) 는 간단히 말해서 가산가법성이다. 주의해야할 점은 서로소인 집합에 대해서만 성립한다는 것이다.
부호측도와 측도를 같이 언급할 때는 강조를 위해서 측도를 양측도positive measure라고 부르기도 한다.
성질
$(X,\mathcal{E},\mu)$를 측도 공간이라 하자.
(A) 단조성: $E,F\in \mathcal{E}$이고 $E\subset F$이면, $\mu (E) \le \mu (F)$이다.
(B) 가산준가법성: $\left\{ E_{j} \right\}_{1}^\infty$가 $\mathcal{E}$의 원소들의 수열이면, $\mu \left( \bigcup_{1}^\infty E_{j} \right) \le \sum _{1}^\infty \mu (E_{j})$이다.
(C) 아래로부터의 연속성: $\left\{ E_{j} \right\}_{1}^\infty \subset \mathcal{E}$가 단조증가수열이라고 하자. 다시말해 $E_{1} \subset E_2 \subset \cdots$. 그러면 다음이 성립한다. $$ \mu\left( \bigcup \nolimits _{1}^\infty E_{j} \right)= \lim \limits_{j\rightarrow \infty} \mu (E_{j}) $$
(D) 위로부터의 연속성: $\left\{ E_{j} \right\}_{1}^\infty \subset \mathcal{E}$가 단조감소수열이라고 하자. 다시말해 $E_{1} \supset E_2 \supset \cdots$. 그리고 $\mu (E_{1})<\infty$라고 하자. 그러면 다음이 성립한다. $$ \mu\left(\bigcap \nolimits _{1}^\infty E_{j} \right)= \lim \limits_{j\rightarrow \infty} \mu (E_{j}) $$
증명
(A)
$E \subset F$라고 하자. 그러면 $F=F\setminus E+ E$이다. 이때 $E$와 $F\setminus E$는 서로소이므로 측도의 정의 (c) 에 의해 다음이 성립한다.
$$ \mu (F) = \mu (F\setminus E+ E) = \mu (F\setminus E) + \mu (E) $$
그러면 측도의 정의 (b) 에 의해서 다음이 성립한다.
$$ \mu (F\setminus E) + \mu (E) \ge \mu (E) $$
따라서 다음을 얻는다.
$$ \mu (F) \ge \mu (E) $$
■
(B)
$F_{1}=E_{1}$라고 하자. 그리고 $k>1$에 대해서 $F_{k}=E_{k} \setminus \left( \bigcup_{1}^{k-1} E_{j} \right)$라고 하자. 그러면 각각의 $F_{k}$는 서로소이고 $\bigcup_{1}^n F_{j}=\bigcup_{1}^n E_{j},\ \forall n$이다. 또한 각각의 $j$에 대해서 $F_{j} \subset E_{j}$이다. 따라서 다음이 성립한다.
$$ \mu \left( \bigcup \nolimits_{1}^\infty E_{j}\right)=\mu \left( \bigcup \nolimits_{1}^\infty F_{j}\right)=\sum \limits_{1}^\infty \mu (F_{j}) \le \sum \limits_{1}^\infty\mu (E_{j}) $$
두번째 등호는 측도의 정의 (c) 에 의해서 성립한다. 마지막 부등식은 (A) 에 의해 성립한다.
■
(C)
$E_{0}:= \varnothing$라고 하자. 그리고 $F_{j}=E_{j}\setminus E_{j-1}$라고 하자. 그러면 각각의 $F_{j}$는 서로소이다. 또한 $\bigcup _{1}^\infty F_{j} =\bigcup_{1}^\infty E_{j}$이다. 그러면 다음이 성립한다.
$$ \begin{align*} \mu \left( \bigcup \nolimits_{1}^\infty E_{j}\right) &= \mu \left( \bigcup \nolimits_{1}^\infty F_{j}\right) \\ &= \sum_{1}^\infty \mu (F_{j}) \\ &= \sum \limits_{1}^\infty \mu (E_{j} \setminus E_{j-1} ) \\ &= \lim \limits_{n \rightarrow \infty} \sum \limits_{1} ^n \mu (E_{j}\setminus E_{j-1} ) \\ &= \lim \limits_{n \rightarrow \infty} \mu (E_{n}) \\ &= \lim \limits_{j \rightarrow \infty} \mu (E_{j}) \end{align*} $$
두번째 등호는 측도의 정의 (c) 에 의해서 성립한다.
■
(D)
$F_{j}=E_{1} \setminus E_{j}$라고 하자. 그러면 $F_{1} \subset F_2 \subset \cdots$이다. 또한 $\mu (E_{1})=\mu (F_{j})+\mu (E_{j})$이고, $\bigcup_{1}^\infty F_{j}=E_{1} \setminus \left( \bigcap_{1}^\infty E_{j} \right)$이 성립한다. 그러면 $E_{1}= \bigcup_{1}^\infty F_{j}+\bigcap_{1}^\infty E_{j}$이므로 다음이 성립한다.
$$ \begin{align*} \mu (E_{1}) &= \mu \left( \bigcap \nolimits_{1}^\infty E_{j}\right) + \mu \left( \bigcup \nolimits _{1}^\infty F_{j} \right) \\ &= \mu \left( \bigcap \nolimits_{1}^\infty E_{j}\right) + \lim \limits_{j \rightarrow \infty} \mu ( F_{j} ) \\ &= \mu \left( \bigcap \nolimits_{1}^\infty E_{j}\right) + \lim \limits_{j \rightarrow \infty}\big[ \mu ( E_{1} )-\mu (E_{j}) \big] \\ &= \mu ( E_{1} )+ \mu \left( \bigcap \nolimits_{1}^\infty E_{j}\right) -\lim \limits_{j \rightarrow \infty}\mu (E_{j}) \end{align*} $$
두번째 등호는 (C) 에 의해서 성립한다. $\mu (E_{1}) < \infty$이므로 다음을 얻는다.
$$ \mu \left( \bigcap \nolimits_{1}^\infty E_{j}\right) = \lim \limits_{j \rightarrow \infty}\mu (E_{j}) $$
■
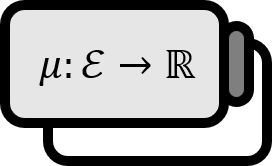
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

