有界線形作用素の拡張定理
定理1 2
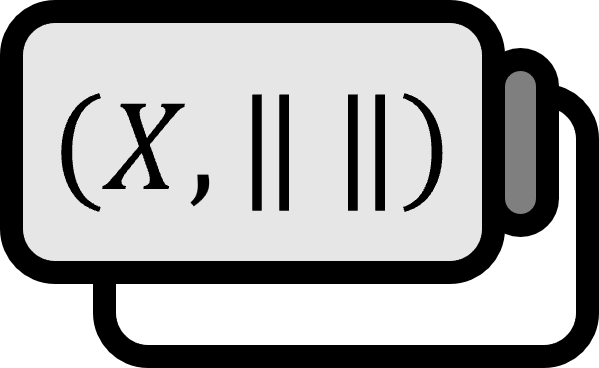
$V_{1}, V_{2}$をバナッハ空間としよう。$W \subset V_{1}$を稠密部分空間としよう。そして、$T : W \to V_{2}$を有界線形作用素としよう。すると、すべての$\mathbf{v} \in W$に対して$\widetilde{T}(\mathbf{v}) = T(\mathbf{v})$を満たす有界線形作用素
$$ \widetilde{T} : V_{1} \to V_{2} $$
が唯一に存在する。また、次のことが成り立つ。
$$ \| \widetilde{T} \| = \left\| T \right\| $$
説明
$\widetilde{T}$を$T$の拡張という。
定理では$\widetilde{T}$の具体的な姿は言及されないが、証明過程で稠密な部分空間を通じて列の収束によって定義される。このようにして拡張した作用素$\widetilde{T}$は自然に$T$として使用されることもある。
有界線形作用素$T : W \to V$と$\mathbf{w} \in \overline{W}\setminus W$がある場合、$T \mathbf{w}$を定義したいが、$T$の定義域が$W$に限られているため不可能である。このとき、$\mathbf{w}$に収束する列$\left\{ \mathbf{w}_{k} \right\}$は$W$に存在するため、$T \mathbf{w}$を「間接的」に次のようにそれらしく定義することができる。
$$ T (\mathbf{w}) := \lim \limits_{k \to \infty} T(\mathbf{w}_{k}) $$
これを言葉で表すと、以下のようになる。
$\mathbf{w}$は、もともと$T$の定義域に属していないため、$T \mathbf{w}$を定義することはできない。しかし、$\mathbf{w}$に収束する列$\left\{ \mathbf{w}_{k} \right\}$が$T$の定義域内に存在する。したがって、$\mathbf{w}_{k} \to \mathbf{w}$の時$T \mathbf{w}_{k} \to T \mathbf{w}$になるため、$T \mathbf{w} := \lim\limits_{k\to \infty}T \mathbf{w}_{k}$のように定義するのは自然であり、それらしい。そして、これが実際に可能である。
したがって、あるバナッハ空間$W$で定義された有界線形作用素$T : W \to V$は、$W$から$V$へのマッピングを保ちながら、$W$の閉包$\overline{W}$まで、上記の定理から定義域を拡張することが保証される。
証明
$\mathbf{v} \in V_{1}$としよう。$W$が$V_{1}$で稠密であるとすると、$\mathbf{v}$に収束する列$\left\{ \mathbf{v}_{k} \right\}$が存在する。
$$ \lim \limits_{k \to \infty} \mathbf{v}_{k} = \mathbf{v} $$
$T$が有界かつ線形であるため、$\ell, k \in \N$に対して次のことが成り立つ。
$$ \left\| T \mathbf{v}_{k} - T \mathbf{v}_{\ell} \right\| = \left\| T (\mathbf{v}_{k} - \mathbf{v}_{\ell}) \right\| \le \left\| T \right\| \left\| \mathbf{v}_{k} - \mathbf{v}_{\ell} \right\| $$
この時、$\left\{ \mathbf{v}_{k} \right\}$がコーシー列であるため、上の式によって$\left\{ T \mathbf{v}_{k} \right\}$もコーシー列になる。したがって、$V_{2}$がバナッハ空間であるため、$\left\{ T \mathbf{v}_{k} \right\}$は$V_{2}$内の何らかの元に収束することになる。ここから、$\widetilde{T}$を次のように定義しよう。
$$ \widetilde{T} \mathbf{v} := \lim \limits_{k \to \infty} T\mathbf{v}_{k} $$
すると、すべての$\mathbf{v} \in W$に対して有界線形作用素の性質により$T \mathbf{v}_{k} \to T \mathbf{v}$が成立するため、$\widetilde{T} \mathbf{v} = T \mathbf{v}$を満たす。今$\mathbf{v} \in V_{1}\setminus W$の場合について考えよう。
パート1. 列の選択の無関係性
$\mathbf{v}$に収束する$W$の二つの列$\left\{ \mathbf{v}_{k} \right\}, \left\{ \mathbf{u}_{k} \right\}$を考えよう。もし、$\mathbf{v}$が$W$内の元であったならば、$T$が有界線形作用素であるため、$\mathbf{v}_{k}, \mathbf{u}_{k} \to \mathbf{v} \in W$の時$T \mathbf{v}_{k}$と$T \mathbf{u}_{k}$が同じ値$T \mathbf{v}$に収束することが保証される。しかし、$\mathbf{v}_{k}, \mathbf{u}_{k} \to \mathbf{v} \in V_{1}\setminus W$の場合には、この性質を使うことができず、直接同じ値に収束するかを確認する必要がある。
今、次のような列$\left\{ \mathbf{w}_{k} \right\}$を考えよう。
$$ \left\{ \mathbf{w}_{k} \right\} = \left\{ \mathbf{v}_{1}, \mathbf{u}_{1}, \mathbf{v}_{2}, \mathbf{u}_{2}, \dots \right\} $$
すると$\lim \limits_{k \to \infty} \mathbf{w}_{k} = \mathbf{v}$が成立し、$T \mathbf{w}_{k}$も何らかの値$\widetilde{T} \mathbf{v} = \lim \limits_{k \to \infty} T\mathbf{w}_{k}$に収束する。しかし、$T \mathbf{v}_{k}$と$T \mathbf{u}_{k}$は$T\mathbf{w}_{k}$の部分列であるため、両者は同じ極限値を持たなければならない。したがって、$\mathbf{v}$に収束する任意の列を取ってきても、$\widetilde{T} \mathbf{v}$は唯一に決定される。
パート2. 線形性
$\mathbf{v}, \mathbf{w} \in V_{1}$であり、$\mathbf{v}_{k} \to \mathbf{v}, \mathbf{w}_{k} \to \mathbf{w}$としよう。
$$ \begin{align*} \widetilde{T} \left( \alpha \mathbf{v} + \beta \mathbf{w} \right) =&\ \lim \limits_{k \to \infty} T \left( \alpha \mathbf{v}_{k} + \beta \mathbf{w}_{k} \right) \\ =&\ \alpha \lim \limits_{k \to \infty} T ( \mathbf{v}_{k} ) + \beta \lim \limits_{k \to \infty} T ( \mathbf{w}_{k} ) \\ =&\ \alpha \widetilde{T} \left(\mathbf{v}\right) + \beta \widetilde{T} \left(\mathbf{w} \right) \end{align*} $$
パート3. 有界、$\| \widetilde{T} \| = \left\| T \right\|$
$\mathbf{v} \in V_{1}$とし、$\mathbf{v}_{k} \to \mathbf{v}$としよう。ノルムは連続であるため、極限を交換できる。この事実と$T$が有界であることを利用すると、
$$ \begin{align*} \left\| \widetilde{T} \mathbf{v} \right\| =&\ \left\| \lim \limits_{k \to \infty} T \mathbf{v}_{k} \right\| \\ =&\ \lim \limits_{k \to \infty} \left\| T \mathbf{v}_{k} \right\| \\ \le& \lim \limits_{k \to \infty} \left\| T \right\| \left\| \mathbf{v}_{k} \right\| \\ =&\ \left\| T \right\| \left\| \lim \limits_{k \to \infty} \mathbf{v}_{k} \right\| \\ =&\ \left\| T \right\| \left\| \mathbf{v} \right\| \end{align*} $$
したがって、$\widetilde{T}$は有界であり、$\| \widetilde{T} \| \le \left\| T \right\|$が成立する。これから、反対向きの不等式が成立することを示そう。$\mathbf{v} \in W$のベクトルに対しては、次のことが成り立つ。
$$ \| \widetilde{T} \mathbf{v} \| = \| T \mathbf{v} \| \le \| T \| \| \mathbf{v} \| $$
しかし、$\mathbf{v} \in V_{1} \setminus W$の場合には、上のように$\| T \|$によってバウンドされないベクトルが存在する可能性がある。したがって、$\| \widetilde{T} \| \ge \left\| T \right\|$が成立することがわかる。したがって、両側の不等式が成立するため、次のことを得る。
$$\| \widetilde{T} \| = \left\| T \right\|$$
■