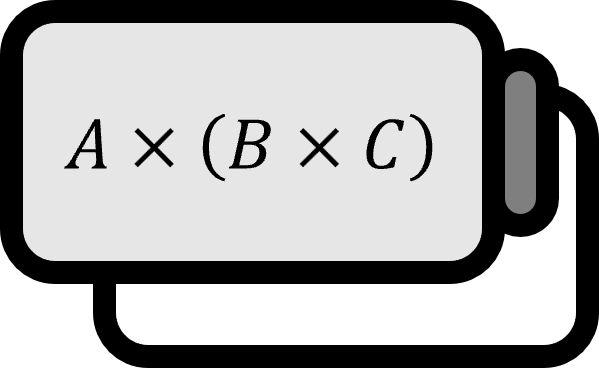直交座標系におけるベクトル関数の発散
定義
ベクトル関数 $\mathbf{F}(x,y,z)=F_{x}\hat{\mathbf{x}}+F_{y}\hat{\mathbf{y}} + F_{z}\hat{\mathbf{z}}$について、以下のようなスカラー関数を$\mathbf{F}$のダイバージェンスdivergence, 発散と定義し、$\nabla \cdot \mathbf{F}$と表記する。
$$ \begin{equation} \nabla \cdot \mathbf{F} := \frac{ \partial F_{x}}{ \partial x} + \frac{ \partial F_{y}}{ \partial y }+ \frac{ \partial F_{z}}{ \partial z} \label{divergence} \end{equation} $$
説明
幾何学的に$\nabla \cdot \mathbf{F}>0$の場合、$\mathbf{F}$が広がり出る、外へ出る形をしていることを意味し、$\nabla \cdot \mathbf{F}<0$の場合は$\mathbf{F}$が集まる、内へ入る形をしていることを意味し、$\nabla \cdot \mathbf{F}=0$の場合は$\mathbf{F}$が広がりも集まりもしない、出入りの量が同じ形をしていることを意味する。
ダイバージェンスは発散と翻訳される。生エビ寿司屋では、勾配をグラディエント、回転をカールと使うため、統一感のために発散ではなくダイバージェンスと表記する。
定義で$\dfrac{ \partial F_{x}}{ \partial x} + \dfrac{ \partial F_{y}}{ \partial y }+ \dfrac{ \partial F_{z}}{ \partial z}$という値を$\nabla \cdot \mathbf{F}$で表記することに注意しよう。$\nabla$をデル演算子と呼ぶことはあるが、これ自体に何か意味を持つと考えると$\nabla \cdot \mathbf{F}$や$\nabla \times \mathbf{F}$を内積と外積と間違えやすい。だから$\nabla$は単なる便利な表記法程度にしか理解しないほうがよく、グラディエント、ダイバージェンス、カールをまとめてデル演算子たちと呼んだり、むしろデル演算子=グラディエントと考えるほうがよいかもしれない。詳細は以下で続ける。
注意点
$\nabla \cdot \mathbf{F}$は$\nabla$と$\mathbf{F}$の内積ではない
内積は基本的に二つのベクトル同士の演算である。$\nabla \cdot \mathbf{F}$を内積と考えることは、$\nabla$を以下のようなベクトルと見なすことである。
$$ \nabla \overset{?}{=}\dfrac{ \partial }{ \partial x}\hat{\mathbf{x}} +\dfrac{ \partial }{ \partial y}\hat{\mathbf{y}}+\dfrac{ \partial }{ \partial z}\hat{\mathbf{z}} = \left( \dfrac{ \partial }{ \partial x},\ \dfrac{ \partial }{ \partial y},\ \dfrac{ \partial }{ \partial z} \right) $$
確かにこのように考えると、次のようにダイバージェンスの定義$(1)$通りに計算がうまくいくので便利であることは事実である。
$$ \nabla \cdot \mathbf{F} = \left( \dfrac{ \partial }{ \partial x},\ \dfrac{ \partial }{ \partial y},\ \dfrac{ \partial }{ \partial z} \right) \cdot \left( F_{x}, F_{y}, F_{z} \right) = \frac{ \partial F_{x}}{ \partial x} + \frac{ \partial F_{y}}{ \partial y }+ \frac{ \partial F_{z}}{ \partial z} $$
しかし、これが実際に内積であれば、内積は交換法則が成立するため、以下のような等式が成立するという奇妙な結論になる。
$$ \mathbf{F} \cdot \nabla = F_{x} \dfrac{\partial }{\partial x} + F_{y} \dfrac{\partial }{\partial y} + F_{z} \dfrac{\partial }{\partial z} \overset{?}{=} \frac{ \partial F_{x}}{ \partial x} + \frac{ \partial F_{y}}{ \partial y }+ \frac{ \partial F_{z}}{ \partial z} = \nabla \cdot \mathbf{F} $$
実際には$\nabla \cdot$の実体はベクトル関数 $\mathbf{F}(x,y,z)$をスカラー関数 $\frac{ \partial F_{x}(x,y,z)}{ \partial x} + \frac{ \partial F_{y}(x,y,z)}{ \partial y }+ \frac{ \partial F_{z}(x,y,z)}{ \partial z}$に対応させる演算子である。これが何を意味するかというと、$\operatorname{div}$という関数を次のように定義してみよう。
$$ \operatorname{div}(\mathbf{F}) := \frac{ \partial F_{x}}{ \partial x} + \frac{ \partial F_{y}}{ \partial y }+ \frac{ \partial F_{z}}{ \partial z},\qquad \mathbf{F} = (F_{x}, F_{y}, F_{z}) $$
ここには内積だとかそういう言葉は一切ない。$\operatorname{div}$という関数は単に変数$\mathbf{F}$が代入されるたびに$\dfrac{ \partial F_{x}}{ \partial x} + \dfrac{ \partial F_{y}}{ \partial y }+ \dfrac{ \partial F_{z}}{ \partial z}$を与える関数である。これを定義してみると、$\nabla$というものを$\nabla = \dfrac{ \partial }{ \partial x}\hat{\mathbf{x}} +\dfrac{ \partial }{ \partial y}\hat{\mathbf{y}}+\dfrac{ \partial }{ \partial z}\hat{\mathbf{z}}$と同じベクトルと考えると$\operatorname{div}$の関数値を表記するのが非常に便利で直感的であることがわかる。だから$\operatorname{div}(\mathbf{F})$と表記する代わりに、$\nabla \cdot \mathbf{F}$と表記するのである。実際に専門の数学の教科書では、ダイバージェンスを$\operatorname{div}$と表記することが容易に見つかるが、これは物理学部と異なり3次元ベクトルを直感的に扱わないためであると考えられる。
では$\nabla \cdot \mathbf{F}$を交換法則が成立しない内積として考えてはいけないのか?
いけない。なぜなら$\nabla \cdot \mathbf{F}$で$\nabla \cdot$自体が関数(演算子)であり$\mathbf{F}$が変数である。一方で$\mathbf{F} \cdot \nabla$はそのもの自体が関数(演算子)であるためである。したがって$\nabla \cdot \mathbf{F}$は関数$\nabla \cdot$の関数値であり、$\mathbf{F} \cdot \nabla$は(まだ変数が代入されていない)関数である。具体的に$\mathbf{F} \cdot \nabla$という表記は次のような関数$f$を直感的
に簡単に表記したものである。$f$はベクトル関数$\mathbf{A}$を変数とする演算子であり、$\mathbf{A}$の各成分に$\left( F_{x}\dfrac{\partial }{\partial x} + F_{y}\dfrac{\partial }{\partial y} + F_{z}\dfrac{\partial }{\partial z} \right)$を適用する関数である。
$$ \begin{align*} f (\mathbf{A}) \overset{\text{definition}}{=}& \left( F_{x}\dfrac{\partial A_{x}}{\partial x} + F_{y}\dfrac{\partial A_{x}}{\partial y} + F_{z}\dfrac{\partial A_{x}}{\partial z} \right)\hat{\mathbf{x}} \\ &\quad+ \left( F_{x}\dfrac{\partial A_{y}}{\partial x} + F_{y}\dfrac{\partial A_{y}}{\partial y} + F_{z}\dfrac{\partial A_{y}}{\partial z} \right)\hat{\mathbf{y}} \\ &\quad+ \left( F_{x}\dfrac{\partial A_{z}}{\partial x} + F_{y}\dfrac{\partial A_{z}}{\partial y} + F_{z}\dfrac{\partial A_{z}}{\partial z} \right)\hat{\mathbf{z}} \\ \overset{\text{notation}}{=}& (\mathbf{F}\cdot \nabla) (\mathbf{A}) \end{align*} $$
何かスカラー関数$\phi$が変数としてある場合、次のような演算子と考える。
$$ \begin{align*} f (\phi) \overset{\text{definition}}{=}& F_{x}\dfrac{\partial \phi}{\partial x} + F_{y}\dfrac{\partial \phi}{\partial y} + F_{z}\dfrac{\partial \phi}{\partial z} \\ \overset{\text{notation}}{=}& (\mathbf{F}\cdot \nabla) (\phi) \end{align*} $$
したがって$\nabla \cdot \mathbf{F}$と$\mathbf{F}\cdot \nabla$は$\nabla$と$\mathbf{F}$の内積として理解してはいけず、$\nabla \cdot$と$\mathbf{F} \cdot \nabla$自体を一つの関数として考えなければならない。これはもちろんダイバージェンスに限った説明ではなく、グラディエント$\nabla f$やカール$\nabla \times \mathbf{F}$も同様に理解しなければならない。
導出
まず以下のように3次元空間で微小体積を考えてみよう。
今、我々の目的は$\mathbf{F}$がその微小体積内の各座標でどのように見えるかを知ることである。現実に例えるならば$\mathbf{F}$が熱であればどの方向に、どの速度で流れているかを、$\mathbf{F}$が水であればこれが蛇口から出ている水なのか、排水溝に入っていく水なのかを知りたいということである。まず$x$軸方向だけを計算してみよう。$\mathbf{F}$が$d\mathbf{a}_{1}$を通過する量は二つのベクトルの内積で求めることができる。
$$ \begin{align} \mathbf{F}(x+dx) \cdot d\mathbf{a}_{1} &= \left( F_{x}(x+dx)\hat{\mathbf{x}}+F_{y}(x+dx)\hat{\mathbf{y}}+F_{z}(x+dx)\hat{\mathbf{z}} \right) \cdot dydz\hat{\mathbf{x}} \nonumber \\ &= F_{x}(x+dx)dydz \end{align} $$
$F_{x}(x+dx)dydz >0$の場合、$\mathbf{F}$が微小体積を抜け出る量であり、$F_{x}(x+dx)dydz<0$の場合は$\mathbf{F}$が微小体積に入る量である。同様に$\mathbf{F}$が$d\mathbf{a}_{2}$を抜け出る量は以下のようである。
$$ \begin{equation} \mathbf{F}(x) \cdot d \mathbf{a}_{2} = F_{x}(x)\hat{\mathbf{x}} \cdot(-dydz\hat{\mathbf{x}})=-F_{x}(x)dydz \end{equation} $$
したがって$(2) + (3)$は微小体積での$\mathbf{F}$の$x$軸方向の流入量(流出量)である。
$$ \begin{align*} (2) + (3) &=\left[ F_{x}(x+dx) -F_{x}(x)\right]dydz \\ &= \frac{F_{x}(x+dx) -F_{x}(x) }{dx}dxdydz \end{align*} $$
しかし$dx$が微小距離であるため、$\dfrac{F_{x}(x+dx) -F_{x}(x) }{dx}\approx \dfrac{ \partial F_{x}}{ \partial x }$と同様に近似できる。したがって$\mathbf{F}$が$x$軸方向へ微小体積に入るまたは出る量は以下のように表される。
$$ \frac{ \partial F_{x}}{ \partial x}dxdydz $$ 同様に$y$軸方向、$z$軸方向について計算すると以下の結果を得る。
$$ \frac{ \partial F_{y}}{ \partial y}dxdydz \quad \text{and} \quad \frac{ \partial F_{z}}{ \partial z}dxdydz $$
これを全て足すと$\mathbf{F}$が微小体積に入るまたは出る量となり、$dxdydz$で割ると単位体積あたりの流入量(流出量)となる。
$$ \frac{ \partial F_{x}}{ \partial x}+\frac{ \partial F_{y}}{ \partial y}+\frac{ \partial F_{z}}{ \partial z} $$
これからこれを$\mathbf{F}$のダイバージェンスと呼び、$\nabla \cdot \mathbf{F}$と表記しよう。
$$ \nabla \cdot \mathbf{F} := \frac{ \partial F_{x}}{ \partial x}+\frac{ \partial F_{y}}{ \partial y}+\frac{ \partial F_{z}}{ \partial z} $$
■
導出される過程を見ても分かるように、上で述べた通り$\nabla \cdot \mathbf{F}$は絶対に$\nabla$と$\mathbf{F}$の内積ではない。この点に注意しよう。
関連する公式
線形性:
$$ \nabla \cdot (f\mathbf{A}) = f(\nabla \cdot \mathbf{A}) + \mathbf{A} \cdot (\nabla f) $$ $$ \nabla \cdot (\mathbf{A} \times \mathbf{B}) = \mathbf{B} \cdot (\nabla \times \mathbf{A}) - \mathbf{A} \cdot (\nabla \times \mathbf{B}) $$
$$ \nabla \cdot (\nabla T) = \dfrac{\partial^{2} T}{\partial x^{2}} + \dfrac{\partial ^{2} T} {\partial y^{2}} + \dfrac{\partial ^{2} T}{\partial z^{2}} $$ $$ \nabla (\nabla \cdot \mathbf{A} ) $$ $$ \nabla \cdot (\nabla \times \mathbf{A})=0 $$
$$ \int_\mathcal{V} \nabla \cdot \mathbf{ F} dV = \oint _\mathcal{S} \mathbf{F} \cdot d \mathbf{S} $$
$$ \int_{\mathcal{V}} \left[ T \nabla^{2} U + (\nabla T) \cdot (\nabla U) \right] d \tau = \oint_{\mathcal{S}} (T \nabla U) \cdot d \mathbf{a} $$ $$ \int_{\mathcal{V}} \left( T \nabla^{2} U - U \nabla^{2} T \right) d \tau = \oint_{\mathcal{S}} \left( T \nabla U - U \nabla T \right) \cdot d \mathbf{a} $$
$$ \int_{\mathcal{V}}\mathbf{A} \cdot (\nabla f)d\tau = \oint_{\mathcal{S}}f\mathbf{A} \cdot d \mathbf{a}-\int_{\mathcal{V}}f(\nabla \cdot \mathbf{A})d\tau $$