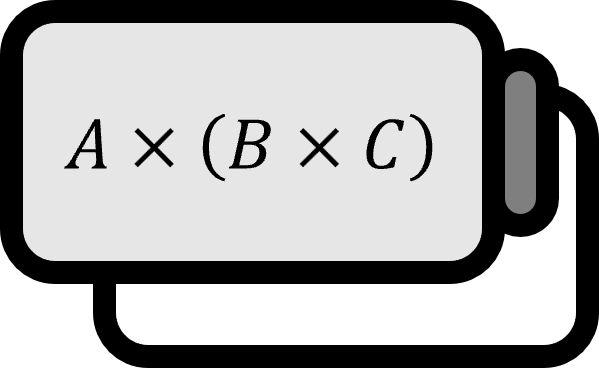3次元デカルト座標系におけるスカラー関数の勾配
定義
スカラー関数 $f=f(x,y,z)$に対して、以下のようなベクトル関数を $f$のグラディエントgradient, 勾配と定義し、$\nabla f$と表記する。
$$ \nabla f := \frac{ \partial f}{ \partial x }\hat{\mathbf{x}}+\frac{ \partial f}{ \partial y}\hat{\mathbf{y}}+\frac{ \partial f}{ \partial z}\hat{\mathbf{z}} = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right) $$
説明
グラディエントは勾配、坂、水勾配などと翻訳される。坂、水勾配はグラディエントの古い翻訳で、最近ではあまり使われない。また、坂は勾配の漢字語であるため、勾配と同じ意味である。グラディエントは実際にベクトルであるため、勾配という言葉はグラディエントが持つ意味をすべて含むには不十分であるように思われる。生しらす寿司店では、勾配という言葉の代わりにグラディエントと統一する。
幾何学的には $\nabla f$は $f$が最も急激に変化する方向を意味する。つまり点 $(x,y,z)$で $f$の増加率が最も大きい方向はベクトル $\left( \dfrac{\partial f(x,y,z)}{\partial x}, \dfrac{\partial f(x,y,z)}{\partial y}, \dfrac{\partial f(x,y,z)}{\partial z} \right)$であるということである。これは微分係数を多次元に拡張したものに過ぎない。$f$が増加していれば微分係数が正、$f$が減少していれば微分係数が負であるという概念と同じである。
一方で定義で $\left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right)$という値を $\nabla f$と表記するとしたことに注意しよう。$\nabla$をデル演算子と呼ぶことはあるが、これ自体に何か意味を持つと考えると$\nabla \cdot \mathbf{F}$や$\nabla \times \mathbf{F}$を内積や外積と誤解するのにちょうどよい。したがって、$\nabla$は単なる便利な表記法としてのみ理解するべきであり、グラディエント、ダイバージェンス、カールをまとめてデル演算子と呼んだり、デル演算子=グラディエントと考える方が良いかもしれない。詳細は以下で続く。
注意点
$\nabla f$は $\nabla$と $f$の積ではない
グラディエントを理解する上で重要なのは、$\nabla f$がベクトル $\nabla = (\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z})$とスカラー $f$の積ではないという事実である。もちろん、そう考えると直感的で良さそうだが、実際は逆である。$\nabla$を $(\frac{\partial }{\partial x}, \frac{\partial }{\
partial y}, \frac{\partial }{\partial z})$というベクトルとして説明することで、ベクトルとスカラーの積のように見えるようにするのである。もし $\nabla f$がベクトル $\nabla$とスカラー $f$の積であれば、ベクトルとスカラーの積は交換可能であるため、次のような奇妙な数式が成り立つことになる。
$$ \nabla f = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right) \overset{?}{=} \left( f\dfrac{\partial }{\partial x}, f\dfrac{\partial }{\partial y}, f\dfrac{\partial }{\partial z} \right) = f\nabla $$
この奇妙な数式が飛び出したのは、実際には $\nabla$はベクトルではなく、$\nabla f$はベクトルとスカラーの積ではないためである。$\nabla$はベクトルではなく、$f(x,y,z)$というスカラー関数を $\left( \frac{\partial f(x,y,z)}{\partial x}, \frac{\partial f(x,y,z)}{\partial y}, \frac{\partial f(x,y,z)}{\partial z} \right)$というベクトル関数に対応させる演算子である。関数自体を変数とする $\operatorname{grad}$という関数を次のように定義してみよう。
$$ \begin{equation} \operatorname{grad} (f) = \left( \dfrac{\partial f}{\partial x}, \dfrac{\partial f}{\partial y}, \dfrac{\partial f}{\partial z} \right), \quad f=f(x,y,z) \end{equation} $$
この定義から、ベクトルとスカラーの積という説明は必要ない。$\operatorname{grad}$は単に変数として $f$が入力されると、$(1)$の規則に従って関数値を持つ関数(演算子)に過ぎない。しかし $\operatorname{grad} (f)$の関数値をよく見ると、$\operatorname{grad} = \nabla$と表記し、これを $\nabla = (\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z})$というベクトルとして説明すると直感的で便利な表記法になるのである。
これは本質的な意味を正確に説明するものではないが、計算や理解の便利さのために使われる他の表記法には微分のライプニッツ表記法がある。$\dfrac{dy}{dx}$という表記法を採用し、分数のように扱うと、変化率という意味を理解するのに便利で、無意識に掛け算や約分などの計算をしても実際の結果とピタリと合う。しかし、皆さんは $\dfrac{dy}{dx}$は分数ではないことを知っている。そう見えるだけで、そう扱うと計算が便利なだけである。$\nabla f$も同様に、ベクトルとスカラーの積に見えるだけで、そう扱うと計算が便利なのであって、実際にそうであるわけではない。
では $f\nabla$は何か?
上の説明に従えば、$\nabla$は一つの関数であるため、$\nabla f = \nabla(f)$は $\nabla$という関数に $f$という変数を代入したときに得られる関数値である。一方で $f \nabla$はそれ自体が一つの関数であり、$g$という関数を変数として代入したときに以下のように関数値を対応させる関数(演算子)である。
$$ (f\nabla) (g) = f\left( \dfrac{\partial g}{\partial x}, \dfrac{\partial g}{\partial y}, \dfrac{\partial g}{\partial z} \right) = \left( f\dfrac{\partial g}{\partial x}, f\dfrac{\partial g}{\partial y}, f\dfrac{\partial g}{\partial z} \right) $$
もちろん、$f \nabla g$
という関数値を見たときには、$f \nabla$に $g$を代入したものと考えても良いし、スカラー関数 $f$とベクトル関数 $\nabla g$の積と見ても良い。
導出
1次元

上の図を見よう。$f_{1}$の点 $x=2$での微分係数は $4$である。$4$という値は関数 $f_{1}$が点 $x=2$でどれほど傾いているかを教えてくれる量だけでなく、それだけではない。$4$の前にある $+$という符号が $f_{1}$のグラフは $x$が増加する方向に増加するという事実も教えてくれる。したがって、微分係数 $4$は単なるスカラーではなく、1次元ベクトル $4\hat{\mathbf{x}}$として理解すべきである。

同様に、$f_{2}$の $x=2$での微分係数は $-3$であり、これは傾きの程度が $3$であることと、$x$が増加する方向に進むと $f_{2}$のグラフが減少するという意味も含んでいる。つまり、符号を方向と考えた場合、微分係数の方向は関数のグラフが大きくなる方向を向いているという話である。別の言い方をすると、微分係数が指し示す方向に進めば、グラフの頂点を見つけることができるということである。
3次元に拡張する前に、$y$の $x$での微分係数 $\dfrac{ d y}{ d x}=a$をまるで分数のように扱えることを思い出そう。これは微分を数学的に厳密に扱う方法ではないが、幾何学的な意味を理解する上での助けとなり、その利点がある。ライプニッツは $dy$、$dx$を $y$と $x$の非常に小さな変化量、微分素と考え、その変化量の比率を微分係数と呼んだ。1
$$ dy=adx $$
余談だが、このように考えるとなぜ $a$を微分 ‘係数’と呼ぶのか理解できる。
3次元
ここで3次元スカラー関数 $f=f(x,y,z)$と位置ベクトル $\mathbf{r}=x\hat{\mathbf{x}}+y\hat{\mathbf{y}}+z\hat{\mathbf{z}}$が与えられたとしよう。$f$の変化量は全微分で表される。
$$ \begin{equation} df=\frac{ \partial f}{ \partial x }dx + \frac{ \partial f}{ \partial y}dy+\frac{ \partial f}{ \partial z}dz \end{equation} $$
$\mathbf{r}$の変化量は以下のようである。
$$ d\mathbf{r}=dx\hat{\mathbf{x}}+dy\hat{\mathbf{y}}+dz\hat{\mathbf{z}} $$
これで1次元の時と同じように、$df$と $d\mathbf{r}$の間の比率を表す何かを探してみよう。しかし、$df$はスカラーで $d\mathbf{r}$はベクトルであるため、その ‘何か’はベクトルであり、$df$はその何かと $d\mathbf{r}$の内積として表現されることを想像できる。したがって
、とりあえずその何かを $\mathbf{a}=a_{1}\hat{\mathbf{x}}+a_{2}\hat{\mathbf{y}}+a_{3}\hat{\mathbf{z}}$と表記して、以下のように表現してみよう。
$$ \begin{align*} df=\mathbf{a}\cdot d\mathbf{r}&=(a_{1}\hat{\mathbf{x}}+a_{2}\hat{\mathbf{y}}+a_{3}\hat{\mathbf{z}})\cdot(dx\hat{\mathbf{x}}+dy\hat{\mathbf{y}}+dz\hat{\mathbf{z}}) \\ &= a_{1}dx+a_{2}dy+a_{3}dz \end{align*} $$
これを $(2)$と比較すると、以下の結果を得る。
$$ \mathbf{a}=\frac{ \partial f}{ \partial x}\hat{\mathbf{x}}+\frac{ \partial f}{ \partial y}\hat{\mathbf{y}}+\frac{ \partial f}{ \partial z}\hat{\mathbf{z}} $$
これから、このベクトル $\mathbf{a}$を $\nabla f$と表記し、$f$のグラディエントと呼ぶことにしよう。グラディエントの方向は関数 $f$のグラフが最も大きく増加する方向を指し、その大きさはその程度を示す。
関連する公式
線形性:
$$ \nabla (f + g) = \nabla f + \nabla g $$
$$ \nabla{(fg)}=f\nabla{g}+g\nabla{f} $$ $$ \nabla(\mathbf{A} \cdot \mathbf{B}) = \mathbf{A} \times (\nabla \times \mathbf{B}) + \mathbf{B} \times (\nabla \times \mathbf{A})+(\mathbf{A} \cdot \nabla)\mathbf{B}+(\mathbf{B} \cdot \nabla) \mathbf{A} $$
$$ \nabla \cdot (\nabla T) = \dfrac{\partial^{2} T}{\partial x^{2}} + \dfrac{\partial ^{2} T} {\partial y^{2}} + \dfrac{\partial ^{2} T}{\partial z^{2}} $$ $$ \nabla \times (\nabla T)= \mathbf{0} $$ $$\nabla (\nabla \cdot \mathbf{A} ) $$
$$ T(b)-T(a) = \int _{a}^{b} (\nabla T) \cdot d\mathbf{l} $$
$$ \int_{\mathcal{V}} (\nabla T) d \tau = \oint_{\mathcal{S}} T d \mathbf{a} $$ $$ \int_{\mathcal{V}} \left[ T \nabla^{2} U + (\nabla T) \cdot (\nabla U) \right] d \tau = \oint_{\mathcal{S}} (T \nabla U) \cdot d \mathbf{a} $$ $$ \int_{\mathcal{V}} \left( T \nabla^{2} U - U \nabla^{2} T \right) d \tau = \oint_{\mathcal{S}} \left( T \nabla U - U \nabla T \right) \cdot d \mathbf{a} $$ $$ \int_{\mathcal{S}} \nabla T \times d \mathbf{a} = - \oint_{\mathcal{P}} T d \mathbf{l} $$
$$ \int_{\mathcal{V}}\mathbf{A} \cdot (\nabla f)d\tau = \oint_{\mathcal{S}}f\mathbf{A} \cdot d \mathbf{a}-\int_{\mathcal{V}}f(\nabla \cdot \mathbf{A})d\tau $$ $$ \int_{\mathcal{S}} f \left( \nabla \times \mathbf{A} \right)\mathbf{A} \cdot d \mathbf{a} = \int_{\mathcal{S}} \left[ \mathbf{A} \times \left( \nabla f \right) \right] \cdot d\mathbf{a} + \oint_{\mathcal{P}} f\mathbf{A} \cdot d\mathbf{l} $$