📂バナッハ空間

一様凸性

定義¹

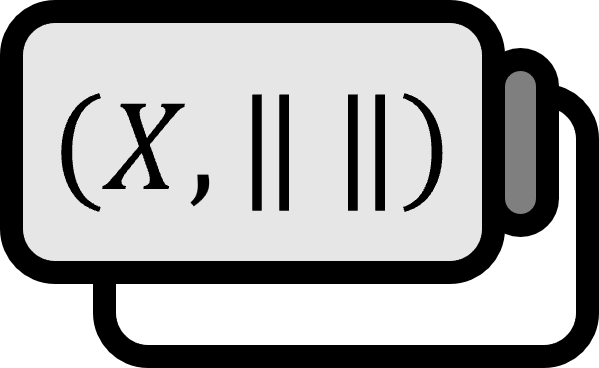
$(X, \left\| \cdot \right\|)$をノルム空間と呼ぼう。$\left\| \cdot \right\|$が以下の条件を満たす場合、$X$のノルム$\left\| \cdot \right\|$は一様に凸^{uniformly convex}だと言う。

• $0 \lt \epsilon \le 2$の全ての$\epsilon$に対して、正数$\delta (\epsilon) \gt 0$が存在して$x,y \in X$で、$\| x \| = \|y\| = 1$かつ$\| x-y\| \ge \epsilon$ならば$\|( x+y)/2 \| \le 1-\delta (\epsilon)$を満たす。

このときノルム空間$X$自体も一様に凸だと言う。もしノルメーブル空間^{normable space}が一様に凸なノルムを持つなら、やはり一様に凸だと言われる。

説明

注意すべき点は、$X$上で定義されたあるノルムが一様に凸だとしても、別の等価なノルム^{another equivalent norm}も一様に凸であるわけではないということだ。

定理

ヒルベルト空間は一様に凸である。

証明

$0< \epsilon \le 2$なる正数$\epsilon$が与えられたとしよう。$H$がヒルベルト空間であり、$x,y \in H$、$\| x\|=\| y\|=1$であり、$\| x-y\| \ge \epsilon$とする。

平行四辺形法則(../1842)

$$ \| x+ y \|^2 + \| x - y \|^2 = 2 \left( \| x \|^2 + \| y \|^{2} \right) $$

$x, y$を平行四辺形法則に代入すると

$$ \| x+ y \|^2 + \| x - y \|^2 = 2 \left( \| x \|^2 + \| y \|^{2} \right) $$

$$ \implies \|x+y\|^2 =4-\|x-y\|^2\le 4-\epsilon^2 $$

$$ \implies \|x+y\|^2\le 4-\epsilon^2 $$

まとめると

$$ \| x+y\| \le \sqrt{4-\epsilon^2} \quad \implies \left\| \frac{x+y}{2} \right\| = \dfrac{1}{2}\|x+y \| \le \frac{1}{2}\sqrt{4-\epsilon^2} $$

このとき$0 \lt \epsilon \le 2$なので、右辺の範囲は$0 \le \dfrac{1}{2}\sqrt{4-\epsilon^2} \lt 1$である。従って、ヒルベルト空間は完備空間なので、ある正数$\delta (\epsilon)$を$\epsilon$に依存して以下のように表せる。

$$ \left\| \frac{x+y}{2} \right\| \le 1-\delta (\epsilon) $$

■