루신의 정리
정리 1
$f : E \to \mathbb{R}$를 가측집합 $E \subset \mathbb{R}$ 위에서 정의된 르벡가측함수라 하자. 그러면 주어진 양수 $\epsilon \gt 0$에 대해, 다음을 만족하는 가측집합 $A \subset \mathbb{R}$가 존재한다.
$$ m(A) \le \epsilon \quad \text{ and } \quad g = f|_{E\setminus A} \text{ is continuous.} $$
여기서 $m$은 르벡측도이다.
일반화2
$f$가 가측함수이고, $A \subset \mathbb{R}^{n}$에 대해서 $\mu (A) \lt \infty$ 이고 $f(x) = 0 \text{ for } x \in A^{c}$라고 하자. 그러면, 주어진 $\epsilon \gt 0$에 대해서, 다음을 만족하는 $g \in$ $C_{c}(\mathbb{R}^{n})$이 존재한다.
$$ \sup\limits_{x\in \mathbb{R}^{n}} g(x) \le \sup\limits_{x \in \mathbb{R}^{n}} f(x) \quad \text{ and } \quad \mu \left( \left\{ x \in \mathbb{R}^{n} : f(x) \ne g(x) \right\} \right) \lt \epsilon $$
설명
이를 루신의 정리Lusin’s theorem라 한다. 한마디로 말해 가측함수 $f$와 거의 같은 연속함수 $g$가 존재한다. 예고로프 정리에 의존하지 않는 증명을 소개한다. 증명에는 위상수학이 사용된다.
증명
실수공간은 제2가산이므로, $\left\{ U_{j} \right\}$를 $\mathbb{R}$의 일반위상의 가산 기저라고 하자. 그리고 $U^{j}$를 다음을 만족하는 열린집합이라 하자.
$$ f^{-1}(U_{j}) \subset U^{j} \quad \text{ and } \quad m(U^{j}\setminus f^{-1}(U_{j})) \lt \dfrac{\epsilon}{2^{j}} $$
여기서 $f^{-1}(U_{j})$는 $U_{j}$의 프리이미지이다. 그리고 $A = \bigcup\limits_{j=1}^{\infty} \left( U^{j} \setminus f^{-1}(U_{j}) \right)$라고 하자. 그러면 $m(A) \lt \epsilon$이 성립한다.
$$ m(A) \lt \epsilon \sum\limits_{j=1}^{\infty}\dfrac{1}{2^{j}} \lt \epsilon $$
이제 $g = f|_{E\setminus A}$가 연속인 것만 보이면 된다. 이를 보이기위해 다음이 성립한다고 가정하자(실제로 성립하는 것을 보이는 건 뒤로 미루겠다).
$$ g^{-1}(U_{j}) = U^{j} \cap \left( E \setminus A \right) \tag{1} $$
이제 $U \subset \mathbb{R}$를 열린집합이라고 하면, $\left\{ U_{j} \right\}$가 기저이므로 $U = \bigcup_{j \in M} U_{j}$를 만족하는 $M$이 존재한다. 그러면 $(1)$에 의해서 다음이 성립한다.
$$ g^{-1}(U) = g^{-1} \bigg( \bigcup_{j \in M} U_{j} \bigg) = \bigcup_{j \in M} g^{-1} \left( U_{j} \right) =\bigg( \bigcup_{j \in M} U^{j} \bigg) \cap \left( E \setminus A \right) $$
열린집합들의 합집합은 열린집합이므로 우변은 $E\setminus A$에서 열린집합이다. 따라서 $g^{-1}(U)$는 열린집합이다. 연속함수일 동치조건에 의해서, 모든 열린집합 $U \subset \mathbb{R}$에 대해서 $g^{-1}(U)$가 열린집합이므로 $g$는 연속이다. 이제 $(1)$을 마저 증명해보자. $g^{-1}(U_{j}) \subset U^{j} \cap \left( E \setminus A \right)$는 정의에 의해 자명하다. 반대방향의 포함관계는 다음의 식으로부터 얻는다.
$$ \begin{align*} U^{j} \cap (E \setminus A)\ \subset\ U^{j} \cap \left( E \setminus [U^{j} \setminus f^{-1}(U_{j})]\right) &= U^{j} \cap \left( E \cap [U^{j} \setminus f^{-1}(U_{j})]^{c}\right) \\ &= U^{j} \cap E \cap [U^{j} \setminus f^{-1}(U_{j})]^{c} \\ &= U^{j} \cap E \cap [ (U^{j})^{c} \cup f^{-1}(U_{j}) ] \\ &= U^{j} \cap E \cap f^{-1}(U_{j}) \\ &= U^{j} \cap f^{-1}(U_{j}) \\ &= f^{-1}(U_{j}) \\ \end{align*} $$
첫번째 등호는 $A \setminus B = A \cap B^{c}$에 의해, 세번째 등호는 $(A \setminus B)^{c} = A^{c} \cup B$에 의해 성립한다. 양변에 $\cap E \setminus A$를 취하면 다음을 얻는다.
$$ U^{j} \cap (E \setminus A) \subset g^{-1}(U_{j}) $$
■
Feldman, Marcus B. A proof of Lusin’s theorem The American Mathematical Monthly 88.3 (1981): 191-192. ↩︎
Robert A. Adams and John J. F. Foutnier, Sobolev Space (2nd Edition, 2003), p15 ↩︎
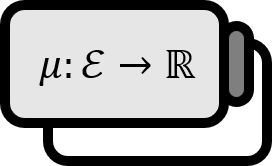
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

