동역학에서의 리우빌 정리 증명
정리
유클리드 공간 $\mathbb{R}^{n}$ 과 함수 $f : \mathbb{R}^{n} \to \mathbb{R}^{n}$ 에 대해 다음과 같은 벡터필드가 미분 방정식으로 주어져 있다고 하자. $$ \dot{x} = f(x) $$ 이 시스템의 플로우 $\phi_t ( \cdot )$ 과 영역 $D_{0} \subset \mathbb{R}^{n}$ 에 대해 $D_{t} := \phi_{t} \left( D_{0} \right)$ 를 플로우에 따라 시간 $t$가 지나 옮겨진 영역, 그 볼륨을 $V(t) \equiv V \left( D_{t} \right)$ 와 같이 나타내자. 만약 $\nabla \cdot f = 0$ 면 모든 $D_{0} \subset \mathbb{R}^{n}$ 와 $t \in \mathbb{R}$ 에 대해 다음이 성립한다. $$ V \left( D_{t} \right) = V \left( D_{0} \right) $$
수식에 대한 설명
$\nabla \cdot f$ 는 벡터필드의 발산으로, 벡터필드가 퍼져나오거나 모여드는 양상을 나타낸다.
$V$ 는 벡터필드에서 주어진 영역의 볼륨을 의미한다.리우빌 정리는 말보다 수식이 더 쉬운데, 쉽게 말해 발산이 어디서나 $0$ 이라면 플로우가 옮긴 영역의 볼륨이 변하지 않는다는 것이다.
증명 1
전략: 벡터 미적분학을 조금 가미하면 된다. 다음과 같이 벡터 함수와 각 벡터의 축을 나타낸다면, 해석학과 선형대수의 기본적인 툴에 따른 계산만으로 직접 연역된다. $$ f := \left( f_{1} , \cdots , f_{n} \right) \\ x := \left( x_{1} , \cdots , x_{n} \right) $$
Part 1. $t_{0} = 0$ 일 때 $\displaystyle \left.{{ d V } \over { d t }}\right|_{t = t_{0}} = \int_{D_{0}} \nabla \cdot f dx$
볼륨의 정의: $\textbf{u} \in \mathbb{R}^{n}$ 가 벡터 함수 $\textbf{f} : \mathbb{R}^{n} \to \mathbb{R}^{n}$ 에 의해 $\textbf{f} \left( \textbf{u} \right) = \left( f_{1} (\textbf{u}) , \cdots , f_{n} (\textbf{u}) \right)$ 와 같이 변환될 때, $D$ 의 볼륨은 다음과 같다. $$ V(D) = \int_{D} \left| {{ \partial \textbf{f} (\textbf{u}) } \over { \partial \textbf{u} }} \right| d u_{1} d u_{2} \cdots d u_{n} $$
볼륨의 정의에 따라 $$ V(t) = \int_{D_{0}} \det {{ \partial \phi_{t} (x) } \over { \partial x }} dx $$ 플로우 $\phi_{t} (x)$ 를 $t=0$ 에서 테일러 전개하면 $$ \phi_{t} (x) = x + f(x) t + O \left( t^{2} \right) $$ $x$ 로 편미분하면 $n\times n$ 단위행렬 $E$ 에 대해 $$ {{ \partial \phi_{t} (x) } \over { \partial x }} = E + {{ \partial f } \over { \partial x }} t + O \left( t^{2} \right) $$ 와 같이 나타낼 수 있다. 그러면 그 행렬식은 $$ \begin{align*} \det {{ \partial \phi_{t} (x) } \over { \partial x }} =& \det \left[ E + {{ \partial f } \over { \partial x }} t \right] + O \left( t^{2} \right) \\ =& 1 + \text{tr} \left[ {{ \partial f } \over { \partial x }} \right] t + O \left( t^{2} \right) \\ =& 1 + \left( {{ d f_{1} } \over { d x_{1} }} + \cdots + {{ d f_{n} } \over { d x_{n} }} \right) t + O \left( t^{2} \right) \\ =& 1 + t \nabla \cdot f + \mathcal{O} \left( t^{2} \right) \end{align*} $$ 여기서 $\text{tr}$ 은 트레이스Trace로, 행렬의 대각성분의 합을 의미한다. 이제 양끝변에 $\int_{D_{0}} \cdot dx$ 를 취하면 $$ \begin{align*} V(t) =& \int_{D_{0}} \det {{ \partial \phi_{t} (x) } \over { \partial x }} dx \\ =& \int_{D_{0}} 1 dx + \int_{D_{0}} t \nabla \cdot f dx + O \left( t^{2} \right) \\ =& V \left( D_{0} \right) + t \int_{D_{0}} \nabla \cdot f dx + O \left( t^{2} \right) \end{align*} $$ $V \left( D_{0} \right) = V(0)$ 을 좌변으로 넘기면 $$ V(t) - V(0) = t \int_{D_{0}} \nabla \cdot f dx + O \left( t^{2} \right) $$ 양변을 $(t - 0)$ 으로 나누면 $$ {{ V(t) - V(0) } \over { t-0 }} = \int_{D_{0}} \nabla \cdot f dx + O \left( t^{1} \right) $$ 테일러 근사를 $t = 0$ 근방에서 사용했으므로 $t \to 0$ 일 때 $O \left( t^{1} \right) \to 0$ 이므로 $$ \left.{{ d V } \over { d t }}\right|_{t = 0} = \int_{D_{0}} \nabla \cdot f dx $$
Part 2. $t = t_{0}$ 으로의 확장
$y := \phi_{t_{0}} (x)$ 이라고 두면 Part 1.에서의 논의를 똑같이 진행해서 다음을 얻는다. $$ \left.{{ d V } \over { d t }}\right|_{t = t_{0}} = \int_{D_{0}} \nabla \cdot f dy $$ 어떤 상수 $c \in \mathbb{R}$ 에 대해 $\nabla \cdot f = c$ 면 $$ \left.{{ d V } \over { d t }}\right|_{t = t_{0}} = \int_{D_{0}} \nabla \cdot f dy = \int_{D_{0}} c dy = c \int_{D_{0}} dy $$ $y$ 는 $x$ 를 시간 $t_{0}$ 만큼 플로우를 따라 보낸 것으로 변환되었으므로 $\int_{D_{0}} dy$ 는 $t_{0}$ 시점의 볼륨이 된다. 이는 임의의 $t_{0} \in \mathbb{R}$ 에 대해서도 마찬가지이므로 $$ V’ = c V $$ 위 미분 방정식은 자명한 솔루션 $V(t) = e^{ct} V (0)$ 를 가진다.
Part 3.
위 **Part 2.**의 마지막 식에서 $c = 0$ 이면 $V(t) = e^{ct} V (0) = V(0)$ 이다.
■
같이보기
Wiggins. (2003). Introduction to Applied Nonlinear Dynamical Systems and Chaos Second Edition(2nd Edition): 99~100. ↩︎
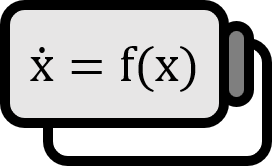
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

