McLeod-Li Test

Hypothesis Testing

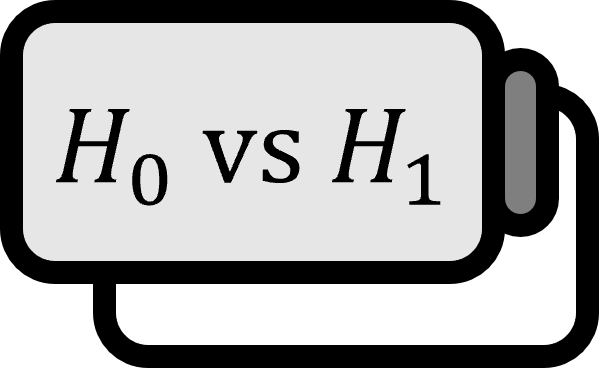
Given the time series data returns $\left\{ r_{t} \right\}$, let’s assume:

$H_{0}$: The data does not exhibit autoregressive conditional heteroscedasticity (ARCH) effect at lag $k$.
$H_{1}$: The data exhibits ARCH effect at lag $k$.

Explanation

McLeod-Li Test is used to check for ARCH effects in the given returns.

Code

Practice

Fortunately, in R, the TSA package’s McLeod.Li.test() function allows for easy testing. This function takes the actual returns of the data, and plots as follows.

The red dashed line represents the significance level $\alpha = 0.05$. The fact that many p-values lie below this line indicates that ‘$H_{0}$: No ARCH effects’ can be rejected, thus it is reasonable to conclude that there are ARCH effects present.

Full Code

library(TSA)
returnize <- function(data) {return(diff(log(data)))}

DAX <- ts(EuStockMarkets[,1],start=1)
r.DAX <- returnize(DAX)

win.graph(6,3)
McLeod.Li.test(y=r.DAX)