📂Banach Space

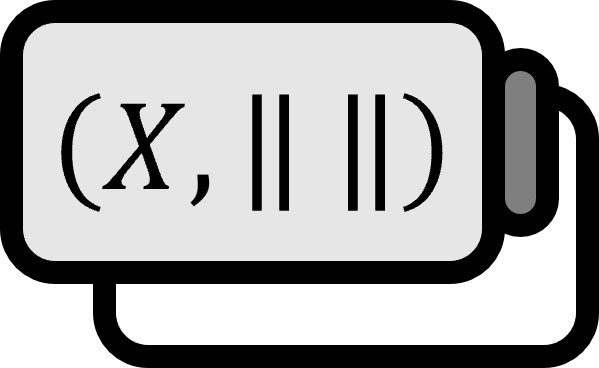
Semi Norm

Definition¹

Let $X$ be a vector space. A function $\left\| \cdot \right\| : X \to \mathbb{R}$ is called a semi norm of $X$ if it satisfies the following three conditions:

(a) $\left\| x \right\| \ge 0,\quad \forall\ x \in X$

(b) $|cx|=|c|\left\| x \right\|,\quad \forall\ x\in X,\ \forall\ c \in\mathbb{C}$

(c) $\left\| x + y \right\| \le \left\| x \right\| + \left\| y \right\|,\quad \forall\ x,y\in X$

Explanation

The definition of a norm without $\left\| x \right\|=0 \iff x = 0$.