📂バナッハ空間

有限次元のノルム空間には基底が存在することの証明

定理 ¹

全ての有限次元ノルム空間は基底を持つ。

説明

特定の条件を満たす基底ではなく、基底の存在を明らかにすることに不慣れかもしれないが、実際に基底の定義で全てのベクトル空間が基底を持つとは一度も言っていない。有限次元を定義するにあたっては、別途証明が不要なほど自明な事実でもある。

証明

戦略: 有限次元であることを利用して具体的に基底を構築する。

---

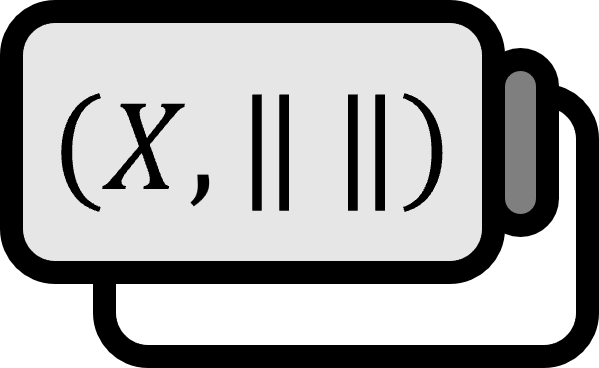
$(X, | \cdot | )$ は有限次元なので$\text{span} \left\{ x_{1} , \dots , x_{n} \right\} = X$ を満たす$\left\{x_{1} , \dots , x_{n} \right\}$ が存在する。$y_{1} : = x_{1}$ とする。もし$x_{2} \in \text{span} \left\{ y_{1} \right\}$ なら$x_{3}$ を考える。もし$x_{2} \notin \text{span} \left\{ y_{1} \right\}$ なら$y_{2} := x_{2}$ とする。もし$x_{3} \in \text{span} \left\{ y_{1}, y_{2} \right\}$ なら$x_{4}$ を考える。もし$x_{3} \notin \text{span} \left\{ y_{1}, y_{2} \right\}$ なら$y_{3} := x_{3}$ とする。このように$M = \left\{ y_{1} , \dots , y_{k} \right\}$ を定義することにより$1 \le j \le k$ に対して

$$ y_{j} \notin \text{span} \left\{ y_{1} , \dots , y_{j-1} \right\} $$

$M$ が線形独立でないと仮定すると、ある$\lambda_{j} \ne 0$たちについて

$$ \lambda_{1} y_{1} + \dots + \lambda_{k} y_{k} = 0 $$

そのような$j$たちの中で最も大きい$j$を$j_{0}$ とする。

$$ y_{j_{0}} = - {{1} \over { \lambda_{j_{0}} }} \sum_{j < j_{0}} \lambda_{j} y_{j} - {{1} \over { \lambda_{j_{0}} }} \sum_{j > j_{0}} \lambda_{j} y_{j} = - {{1} \over { \lambda_{j_{0}} }} \sum_{j < j_{0}} \lambda_{j} y_{j} $$

したがって$\displaystyle y_{j_{0}} = - {{1} \over { \lambda_{j_{0}} }} \sum_{j < j_{0}} \lambda_{j} y_{j} \in \text{span} \left\{ y_{1} , \dots , y_{j_{0}-1} \right\}$で、これは矛盾である。$M \subset \left\{ x_{1} , \dots , x_{n} \right\}$は線形独立であり$\text{span} M = X$を満たすので、$M$は$X$の基底となる。

■

証明過程をよく見ると、$\left\{ x_{1} , \dots , x_{n} \right\}$はかなり余裕を持って$X$を生成することがわかる。線形独立になることを妨げるものをすべて捨てて$M$だけを取り、具体的にそれが基底であることを示したのである。