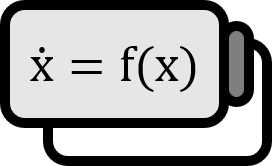📂動力学

非線形システムの線形化

ビルドアップ

空間$\left( X, \left\| \cdot \right\| \right)$と関数$f : X \to X$に関して、以下のようなベクターフィールドが微分方程式として与えられているとしよう。 $$\dot{x} = f(x)$$ このような自律システムの固定点 $\overline{x}$が与えられた場合、その周辺の安定性を把握するためには、線形化という方法が不可欠になる。システム全体を見た際、固定点の近くでは線形に見て分析するということだ。これは多次元非線形マップを扱うアイディアと同じだ。

固定点$\overline{x}$にとても近い点$x$が次のように表されるとしよう。 $$x:= \overline{x} + \xi$$ すると、そのテイラー展開は $$\dot{x} = \overline{x} ' + \xi ' = f \left( \overline{x} \right) + D f \left( \overline{x} \right) \xi + O \left( \left\| \xi \right\|^{2} \right)$$ もちろん$\overline{x} ' = f \left( \overline{x} \right)$であるため、2つ目と3つ目の項を消去し、$\xi '$について整理すると $$\xi ' = D f \left( \overline{x} \right) \xi + O \left( \left\| \xi \right\|^{2} \right)$$ $D$はヤコビアンだ。ここで$\left\| \xi \right\|^{2}$が十分に小さいならば、つまり$x$が$\overline{x}$にとても近いならば、最後の項は無視できる。

定義

このような過程を線形化と呼び、このようにして得られる新しい微分方程式を関連する線形システムという。 $$\xi ' = D f \left( \overline{x} \right) \xi$$

説明

線形化の限界

注意点は、線形化されたシステムでの固定点のリアプノフ安定性が、元のシステムでの安定性までも保証しないということだ。例¹として、以下のような非線形システムの線形化を見てみよう： $$\begin{align*} \dot{x} =& f_{1} (x , y) = -y + x \left( x^{2} + y^{2} \right) \\ \dot{y} =& f_{2} (x , y ) = x + y \left( x^{2} + y^{2} \right) \end{align*}$$ 当然ながら、原点$\overline{(x,y)} = (0,0)$は上記システムの固定点となる。

---

Part 1.

線形システムについて、関連する線形システム$\xi ' = D f \left( \overline{x} \right) \xi$は次のように導出される。 $$\begin{align*} \begin{bmatrix} \xi_{1} \\ \xi_{2} \end{bmatrix} ' =& \begin{bmatrix} {{ \partial f_{1} } \over { \partial x }} & {{ \partial f_{1} } \over { \partial y }} \\ {{ \partial f_{2} } \over { \partial x }} & {{ \partial f_{2} } \over { \partial y }} \end{bmatrix}_{\overline{(x,y)} = (0,0)} \begin{bmatrix} \xi_{1} \\ \xi_{2} \end{bmatrix} \\ =& \begin{bmatrix} 3 x^{2} + y^{2} & -1 + 2 x y \\ 1 + 2x y & x^{2} + 3 y^{2} \end{bmatrix}_{ \overline{(x,y)} = (0,0)} \begin{bmatrix} \xi_{1} \\ \xi_{2} \end{bmatrix} \\ =& \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} \xi_{1} \\ \xi_{2} \end{bmatrix} \end{align*}$$ $\xi ' = D f \left( \overline{x} \right) \xi$をきれいに整理すると、次のようになる。 $$\begin{align*} \xi_{1} ' =& - \xi_{2} \\ \xi_{2} ' =& \xi_{1} \end{align*}$$

---

Part 2. 線形システムでの安定性

線形化されたシステムで$\overline{x}$のリアプノフ安定性を確認してみよう。このシステムのすべてのソリューションはかなりシンプルであることがわかるが、それは$D f \left( \overline{x} \right)$を線形変換と見たとき、行列の形が回転変換であるため、すべての点が原点を中心に一定の距離$r>0$を保ちながら逆時計回りに回転するベクターフィールドだからだ。

リアプノフ安定性の定義：$t_{0} \in \mathbb{R}$としよう。与えられた微分方程式のソリューション$\overline{x}(t)$が$\varepsilon > 0$が与えられるたびに $$\left\| \overline{x} \left( t_{0} \right) - y \left( t_{0} \right) \right\| < \delta \implies \left\| \overline{x}(t) - y(t) \right\| < \varepsilon \qquad , t > t_{0}$$ を満たす別のすべてのソリューション$y(t)$に対して$\delta ( \varepsilon ) > 0$が存在すれば、$\overline{x}(t)$は安定と言われる。

定義に従えば、固定点$\overline{(x,y)} = (0,0)$が安定であるためには $$\left\| \xi (t_{0}) \right\| < \delta \implies \left\| \xi (t) \right\| < \varepsilon \qquad , t > t_{0}$$ が$\varepsilon > 0$が与えられるたびに存在しなければならないが、このシステムのすべての別のソリューションは、時間が経つと関係なく原点と一定の距離を保ちながら回転するため、$\delta (\varepsilon) = \varepsilon$は自明に存在する。したがって、$\overline{(x,y)} = (0,0)$はこの線形システムで安定と言える。

---

Part 3. 非線形システムでの安定性

非線形システムでの安定性を確認する典型的な方法ではないが、この場合、極座標変換を通じて比較的簡単に安定性をチェックできる。以下のように$x, y$を極座標で表すと考えてみよう。

$$x = r \cos \theta \\ y = r \sin \theta$$ すると$r^{2} = x^{2} + y^{2}$なので、両辺を時間$t$に対して微分すると $$\begin{align*} & 2r \dot{r} = 2 x \dot{x} + 2y \dot{y} \\ \implies& r\dot{r} = x \left[ -y + x \left( x^{2} + y^{2} \right) \right] + y \left[ x + y \left( x^{2} + y^{2} \right) \right] \\ \implies& r \dot{r} = r \cos \theta \left[ - r \sin \theta + r \cos \theta \cdot r^{2} \right] + r \sin \theta \left[r \cos \theta + r \sin \theta \cdot r^{2} \right] \\ \implies& r \dot{r} = r^{4} \cos^{2} \theta + r^{4} \sin^{2} \theta \\ \implies& \dot{r} = r^{3} \end{align*}$$ 同様に、極座標変換$x=r \cos \theta$を時間$t$に対して微分すると $$\begin{align*} & \dot{x} = \dot{r} \cos \theta - r \theta^{\prime}\sin \theta \\ \implies& - r \sin \theta + r^{3} \cos \theta = r^{3} \cos \theta - \left( r \sin \theta \right) \dot{\theta} \\ \implies& 1 = \dot{\theta} \end{align*}$$ これを整理すると $$\begin{align*} \dot{r} =& r^{3} \\ \dot{\theta} =& 1 \end{align*}$$ 極座標表現によると、固定点$\overline{(x,y)} = (0,0)$を除くすべての点では$r>0$が保たれるため、したがって$\dot{r}>0$でもある。これは言い換えれば、このシステムの固定点を除くすべてのソリューションは、原点を中心に一定の$\theta$だけ回転し、$r$が次第に大きくなる螺旋を描くということだ。いくら固定点に近くとも、最終的には時間が経つにつれて原点から離れるため、この非線形システムは安定とは言えない。

漸近的安定性

上記の例から、線形システムの安定性が非線形システムの安定性を保証しないことが確認できた。[注意：このような場合も線形安定性と呼ぶことがある。]しかし、双曲線的な固定点の場合はこれが同値となり、線形化は引き続き強力なツールとなる。

関連する線形化システムと漸近的安定性²: $\dot{x} = f(x)$ 의 고정점 $\overline{x}$ 에 대해 $D f (\overline{x})$ 의 모든 고유값들의 실수부가 음수면 $\overline{x}$ 는 점근적 안정성을 가진다.

特にこの定理は広く知られており、動的システムの分析のほとんどに使用されている。その証明には、リアプノフ関数の存在³と線形代数的なトリック⁴が必要だが、これを直接示すことは思ったより簡単ではない。