logo

リウヴィルの定理の証明 📂ヒルベルト空間

リウヴィルの定理の証明

証明

f=0f = 0とする。f(⋅)=⟨⋅,0⟩f ( \cdot ) = \left\langle \cdot , \mathbf{0} \right\rangleと∥f∥=0\| f \| = 0を満たすy=0\mathbf{y} = \mathbf{0}が存在するので証明することはないのでf≠0f \ne 0としよう。

  • 第1部. 存在性

    直交分解定理

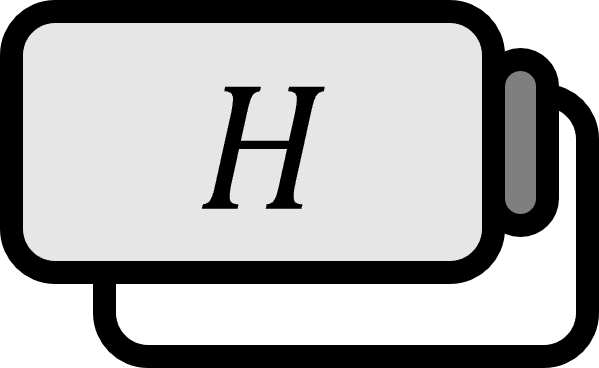
    ヒルベルト空間HHの閉部分空間WWに対して、

    H=W⊕W⊥ H = W \oplus W^{\perp}

    W=ker⁡(f)={x∈H:f(x)=0}W= \ker (f) = \left\{ \mathbf{x} \in H : f(\mathbf{x}) = 0 \right\}としよう。ker⁡(f)\ker (f)は閉部分空間だから直交分解定理によって

    H=W⊕W⊥ H = W \oplus W^{\perp}

    でW⊥≠{0}W^{\perp} \ne \left\{ \mathbf{0} \right\}である。だから∥y∥=1\left\| \mathbf{y} \right\|=1なy∈W⊥\mathbf{y} \in W^{\perp}を一つ選ぼう。W⊥W^{\perp}もベクトル空間なので0\mathbf{0}でない要素が少なくとも一つあれば、そのようなy\mathbf{y}の存在は必ず保証される。そして今x∈H\mathbf{x} \in Hに対して、次のようなベクトルz∈H\mathbf{z} \in Hを考える。

    z:=f(x)y−f(y)x \mathbf{z} := f(\mathbf{x})\mathbf{y} - f(\mathbf{y})\mathbf{x}

    ここでf(x),f(y)f(\mathbf{x}), f(\mathbf{y})は定数であることに注意しよう。このz\mathbf{z}に線形汎函数ffを適用すると、線形性により次を得る。

    f(z)=f(f(x)y−f(y)x)=f(x)f(y)−f(y)f(x)=0 f(\mathbf{z}) = f\left( f(\mathbf{x})\mathbf{y} - f(\mathbf{y})\mathbf{x} \right) = f(\mathbf{x})f(\mathbf{y}) - f(\mathbf{y})f(\mathbf{x}) = 0

    したがってz∈W\mathbf{z} \in Wである。y∈W⊥\mathbf{y} \in W^{\perp}と言ったので、両者の内積は00である。

    ⟨z,y⟩=⟨f(x)y−f(y)x,y⟩=0 \left\langle \mathbf{z}, \mathbf{y} \right\rangle = \left\langle f(\mathbf{x})\mathbf{y} - f(\mathbf{y})\mathbf{x}, \mathbf{y} \right\rangle = 0

    内積を展開すると次を得る。

    f(x)⟨y,y⟩−f(y)⟨x,y⟩=f(x)∥y∥2−f(y)⟨x,y⟩=f(x)−f(y)⟨x,y⟩=0 f(\mathbf{x}) \left\langle \mathbf{y}, \mathbf{y} \right\rangle - f(\mathbf{y})\left\langle \mathbf{x}, \mathbf{y} \right\rangle = f(\mathbf{x}) \left\| \mathbf{y} \right\|^{2} - f(\mathbf{y})\left\langle \mathbf{x}, \mathbf{y} \right\rangle = f(\mathbf{x}) - f(\mathbf{y})\left\langle \mathbf{x}, \mathbf{y} \right\rangle=0

      ⟹  f(x)=f(y)⟨x,y⟩=⟨x,f(y)‾y⟩ \implies f(\mathbf{x}) = f(\mathbf{y})\left\langle \mathbf{x}, \mathbf{y} \right\rangle = \left\langle \mathbf{x}, \overline{f(\mathbf{y})}\mathbf{y} \right\rangle

    w=f(y)‾y\mathbf{w} = \overline{f(\mathbf{y})}\mathbf{y}とするとf(x)=⟨x,w⟩f(\mathbf{x}) = \left\langle \mathbf{x} , \mathbf{w} \right\rangleである。またコーシー・シュワルツの不等式によって ∥f∥=sup⁡∥x∥=1∣f(x)∣=sup⁡∥x∥=1∣⟨x,w⟩∣≤sup⁡∥x∥=1∥x∥⋅∥w∥=∥w∥ \| f \| = \sup_{ \| \mathbf{x} \| =1} | f(\mathbf{x}) | = \sup_{ \| \mathbf{x} \| =1} \left| \left\langle \mathbf{x} , \mathbf{w} \right\rangle \right| \le \sup_{ \| \mathbf{x} \| =1} \| \mathbf{x} \| \cdot \| \mathbf{w} \| = \| \mathbf{w} \|

    であり、∥w∥w∥∥=1\left\| \dfrac{\mathbf{w}}{\left\| \mathbf{w}\right\|} \right\|=1であるので

    ∥f∥=sup⁡∥x∥=1∣f(x)∣=sup⁡∥x∥=1∣⟨x,w⟩∣≥⟨w∥w∥,w⟩=∥w∥2∥w∥=∥w∥ \| f \| = \sup_{ \| \mathbf{x} \| =1} | f(\mathbf{x}) | = \sup_{ \| \mathbf{x} \| =1} \left| \left\langle \mathbf{x} , \mathbf{w} \right\rangle \right| \ge \left\langle {{ \mathbf{w} } \over { \| \mathbf{w} \| }} , \mathbf{w} \right\rangle = {{ \| \mathbf{w} \|^2 } \over { \| \mathbf{w} \| }} = \| \mathbf{w} \|

が成立して∥f∥=∥w∥\left\| f \right\| = \left\| \mathbf{w} \right\|である。従ってw\mathbf{w}が定理の条件を満たしていることがわかる。

  • 第2部. 一意性

    今w′\mathbf{w}^{\prime}も

    f(x)=⟨x,w′⟩ f(\mathbf{x}) = \left\langle \mathbf{x}, \mathbf{w}^{\prime} \right\rangle

    を満たすとしよう。

    補助定理

    (H,⟨⋅,⋅⟩)\left( H, \left\langle \cdot,\cdot \right\rangle \right)をヒルベルト空間とし、x,y∈Hx, y \in Hに対して次が成り立つとしよう：

    ⟨x,y⟩=⟨x,z⟩,∀x∈H \left\langle x, y \right\rangle = \left\langle x, z \right\rangle, \quad \forall x \in H

    するとy=zy = zである。

    それなら、上の補助定理によって、このようなw=w′\mathbf{w}=\mathbf{w}^{\prime}であることがわかる。

■