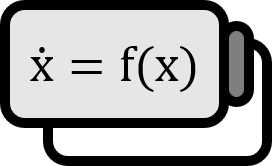📂動力学

自律システムにおける固定点の分類

定義

空間 $X$ と関数 $f \in C^{1}(X,X)$ に対して、以下のようなベクトル場が微分方程式として与えられているとしよう。 $$\dot{x} = f(x)$$ $\overline{x}$ がこの自律系の一つの固定点であり、$D f \left( \overline{x} \right)$ の固有値を $\lambda_{1} , \cdots , \lambda_{m}$ とする。

ハイパーボリック：双曲固定点¹

1. ハイパーボリック：$D f \left( \overline{x} \right)$ の全ての固有値の実部が $0$ でなければ、$\overline{x}$ はハイパーボリックだと言われる。 $$\operatorname{Re} \left( \lambda_{1} \right) \ne 0 , \cdots , \operatorname{Re} \left( \lambda_{m} \right) \ne 0$$
   1. サドル：$\overline{x}$ がハイパーボリックであり、$D f \left( \overline{x} \right)$ が実部が正の固有値と負の固有値を少なくとも一つずつ持つ場合、$\overline{x}$ はサドルだという。 $$\exists i, j \in [1,m] : \operatorname{Re} \left( \lambda_{i} \right) > 0 \land \operatorname{Re} \left( \lambda_{j} \right) < 0$$
   2. シンク：$D f \left( \overline{x} \right)$ の全ての固有値の実部が負ならば、$\overline{x}$ は安定^stableだと言われ、シンクという。 $$\operatorname{Re} \left( \lambda_{1} \right) < 0 , \cdots , \operatorname{Re} \left( \lambda_{m} \right) < 0$$
   3. ソース：$D f \left( \overline{x} \right)$ の全ての固有値の実部が正ならば、$\overline{x}$ は不安定^untableだと言われ、ソースという。 $$\operatorname{Re} \left( \lambda_{1} \right) > 0 , \cdots , \operatorname{Re} \left( \lambda_{m} \right) > 0$$

エリプティック：楕円固定点²

2. エリプティック、センター：$D f \left( \overline{x} \right)$ の全ての固有値が純虚数ならば、$\overline{x}$ はエリプティックだと言われ、センターという。 $$\operatorname{Im} \left( \lambda_{1} \right) = \lambda_{1} , \cdots , \operatorname{Im} \left( \lambda_{m} \right) = \lambda_{m}$$

---

• $\re$ と$\im$ はそれぞれ複素数から実部と虚部を取り出す関数である。

説明

定義ではそう言われていないけれども、ハイパーボリックかどうかは、端的に言って、システムが単純かどうかとほぼ一致する。システムを動力学的に分析する場合、主な問題はほとんどの場合、固有値が $0$ である場合に生じる。ハイパーボリックであれば、そのような厄介ごとを心配せずに済むため、分析も単純になる。

例

例として、ダフィング振り子を考えてみよう： $$\begin{align*} \dot{x} =& y \\ \dot{y} =& x - x^{3} - \delta y \qquad , \delta \ge 0 \end{align*}$$ ダフィング振り子の固定点は $(x,y) = (0,0) , (\pm 1 , 0)$ であり、ヤコビアンは $$D \mathbf{f} = \begin{bmatrix} 0 & 1 \\ 1 - 3 x^{2} & - \delta \end{bmatrix}$$ であるため、固定点でのヤコビアンは $$D \mathbf{f} (0,0) = \begin{bmatrix} 0 & 1 \\ 1 & - \delta \end{bmatrix} \\ D \mathbf{f} (\pm1,0) = \begin{bmatrix} 0 & 1 \\ -2 & - \delta \end{bmatrix}$$ である。これらの固有値を計算すると、$(0,0)$ の時 $$\det ( D \mathbf{f} (0,0) - \lambda E ) = \det \begin{bmatrix} -\lambda & 1 \\ 1 & -\lambda - \delta \end{bmatrix} = \lambda^{2} + \delta \lambda - 1$$ であり、二次方程式の解によって $$\lambda_{1,2} = {{ -\delta \pm \sqrt{\delta^{2} + 4 } } \over { 2 }}$$ である。$D \mathbf{f} (0,0)$ の固有値は常に正数と負数の一つずつを持つため、固定点 $(0,0)$ はサドルである。同様に、$D \mathbf{f} (\pm1,0)$ の固有値を計算すると $$\lambda_{1,2} = {{ -\delta \pm \sqrt{\delta^{2} - 8 } } \over { 2 }}$$ であるため、$D \mathbf{f} (\pm1,0)$ の固有値は $\delta > 0$ の時、全部負であり、固定点 $(\pm1,0)$ はシンクである。しかし、$\delta = 0$ の時は純虚数 $\lambda_{1,2} = \pm \sqrt{2} i$ であるため、固定点 $(\pm1,0)$ はセンターである。

上記の例では、各固定点でヤコビアンを求め、パラメーター $\delta$ の設定によって安定性がどのように変化するかを見た。このような分析は、システムがベクトル場で表されていれば、動力学のどの論文でも同じように使われる方法である。少なくとも一度は、必ず自分で試してみよう。