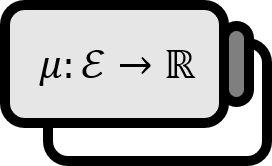Methods of Expressing an Arbitrary Function as Two Non-negative Functions 📂Measure Theory

Methods of Expressing an Arbitrary Function as Two Non-negative Functions

Definitions¹

Let’s define $f^{+}$ and $f^{-}$ for a function $f : X \to \mathbb{R}$ as follows.

$$ \begin{align*} f^{+} (x) &:= \max \left\{ f(x),\ 0 \right\} \\ f^{-} (x) &:= \max \left\{ -f(x),\ 0 \right\} \end{align*} $$

We call $f^{+}$ the positive part of $f$, and $f^{-}$ the negative part of $f$.

Description

Despite their names, both $f^{+}$ and $f^{-}$ are non-negative functions. It might not be immediately clear why these are referred to as the positive and negative parts, respectively. Let’s look at the figure below.

As you can see from the figure, the positive part $f^{+}$ exactly represents the parts where the value of $f$ is positive, and $f^{-}$ represents (as positive values) the parts where the value of $f$ is negative. It’s easy to see that the following formulas hold based on the above definitions.

$$ f=f^{+} -f^{-},\quad |f|=f^{+}+f^{-} $$

$$ \begin{array}{c} f^{+}=\frac{1}{2}(|f| + f),\quad f^{-}=\frac{1}{2}(|f|-f) \end{array} $$

Theorem

(1)

Let’s assume that the three functions $f,g,h : X \to \mathbb{R}$ satisfy the conditions below.

$$ f(x)=g(x)-h(x), \quad \min \left\{ g(x),\ h(x) \right\} \ge 0\ \quad \forall\ x \in X $$

Then, the following formula holds.

$$ f^{+} (x) \le g(x), \quad f^{-} (x) \le h(x) \quad \forall\ x \in X $$

This means that when any function is represented as the difference of two non-negative functions, the positive part $f^{+}$ and the negative part $f^{-}$ of $f$ are the smallest functions that satisfy this.

(2)

If $f$ is a measurable function, then $f^{\pm}$ is also measurable.

Proof

(1)

For any $x$, since $ f(x)=g(x)-h(x)$ and $h(x) \ge 0$, it follows that $f(x) \le g(x)$. Also, by assumption, $0 \le g(x)$. Because $g(x)$ is greater than or equal to both $f(x)$ and $0$, it is also greater than or equal to the larger of the two. Therefore, the following holds.

$$ f^{+}(x) = \max \left\{ f(x), 0 \right\} \le g(x) $$

For any $x$, since $-f(x)=h(x)-g(x)$ and $g(x) \ge 0$, it follows that $-f(x) \le h(x)$. Also, by assumption, $0 \le h(x)$. Because $h(x)$ is greater than or equal to both $-f(x)$ and $0$, it is also greater than or equal to the larger of the two. Therefore, the following holds.

$$ f^{-}(x) = \max \left\{ -f(x), 0 \right\} \le h(x) $$

■