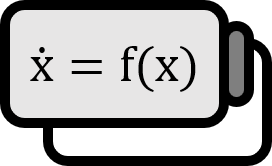📂Dynamics

Lorenz Attractor

Overview

The Lorenz Equation is a mathematical model that represents atmospheric convection as a system of differential equations.

System

$$ \begin{align*} {{dx} \over {dt}} =& - \sigma x + \sigma y \\ {{dy} \over {dt}} =& - xz + \rho x - y \\ {{dz} \over {dt}} =& xy - \beta z \end{align*} $$

Variables

• $x(t)$: Represents the $x$ coordinate of a particle at time $t$.
• $y(t)$: Represents the $y$ coordinate of a particle at time $t$.
• $z(t)$: Represents the $z$ coordinate of a particle at time $t$.

Parameters

• $\sigma$: Known as the Prandtl Number, a parameter related to viscosity and thermal conductivity.
• $\rho$: Known as the Rayleigh Number, a parameter related to the method of heat transfer in fluids.
• $\beta$: According to Wikipedia¹, it seems to be a parameter related to dimensions. Often, textbooks do not precisely explain what it is.

---

In initial simulations, these parameters are often set to $\sigma = 10$, $\rho = 28$, and $\displaystyle \beta = {{8} \over {3}}$, as Lorenz did. When the Rayleigh Number exceeds $\rho \approx 24.74$, the motion of the particle described by the Lorenz Attractor becomes chaotic. It reacts sensitively to even the slightest changes in initial conditions, making prediction very difficult. It’s like a butterfly’s wing could potentially cause a storm.

Explanation

Bifurcation

The above image is a bifurcation diagram of the Lorenz attractor². The horizontal axis shows the value of $\rho$ gradually changing from $25$ to $325$, and the vertical axis marks the maximum values in the $z$ direction from the orbit after a sufficiently long time. When $r= \rho$ is small, the motion appears very unstable, but it becomes stable once it grows beyond a certain level. It is advisable to read the following explanation:

The graph above plots the trajectory when $\gamma=100$. Typically, if $\gamma$ is quite large, the initial movements seem chaotic, but it can become periodic over time.

This graph removes the initial trajectory to show the particle’s path after a long period. Though not completely periodic, its behavior becomes almost predictable.

Plotting the trajectory nicely on a $xz$ graph yields the above shape. Initially chaotic, the trajectory stabilizes over time, clearly showing about three peak values. The same interpretation can be derived from observing the bifurcation diagram.

On the other hand, when $\gamma = 28$, the movement remains chaotic even after a long time. In the bifurcation diagram, several points scatter to form a thickened appearance.

Conversely, when $\gamma = 300$, only two distinct peaks emerge as shown above. In the bifurcation diagram, this results in two lines representing two peaks corresponding to a single value of $\gamma$.

Lyapunov Spectrum

Below is the Lyapunov spectrum at $\rho \in [0, 100]$³.

Code

MATLAB

Below is the code to plot the trajectory of the Lorenz attractor using MATLAB.

sigma = 10;
beta = 8/3;
rho = 28;
f = @(t,v) [-sigma*v(1) + sigma*v(2); rho*v(1) - v(2) - v(1)*v(3); -beta*v(3) + v(1)*v(2)];
[t,v] = ode45(f,[0 10000],[1 1 1]);     % Runge-Kutta 4th/5th order ODE solver
x=v(:,1); x=x(50000:end);
y=v(:,2); y=y(50000:end);
z=v(:,3); z=z(50000:end);
plot3(x,y,z)
%plot(x,z)

Fortran

Below is the Fortran code to generate the source for the bifurcation diagram and output it to a OUTPUT.csv file. The method used to solve the ODE is RK4.

program LorenzBifurcation
  implicit none
  double precision :: sigma=10.d0, rho=28.d0, beta=8.d0/3.d0
  Integer, parameter :: D = 3
  double precision :: v(D)=1.d0, h=0.001d0, z1, z2, z3
  integer :: i, j, k, preitr=10**4-1000, endstep=10**4
  character :: answer
  abstract interface
     function func (v)
       Integer, parameter :: D = 3
       double precision :: v(D), func(D)
     end function func
  end interface
  open(UNIT=34,FILE="OUTPUT.csv",ACTION="WRITE")
  rho=5.d0
  h=0.01d0
  do while(rho<325)
    print '(A,f6.4,A)', "Now", (rho-5.d0)/320.d0, "%"
    do i=1, preitr
       v = RK4(v,f)
    end do
    z1 = preitr
    z2 = preitr
    z3 = preitr
    do i=preitr+1, endstep
       v = RK4(v,f)
       z1 = z2
       z2 = z3
       z3 = v(3)
       if(z1<z2 .and. z2>z3) then
         write (34,*) rho, ",", z2
       end if
    end do
    v=1.d0
    rho=rho+0.1d0
  end do
contains
  function RK4(v,f)
    procedure (func) :: f
    double precision :: v(D), V1(D), V2(D), V3(D), V4(D), RK4(D)
    V1 = f(v)
    V2 = f(v + (h/2)*V1)
    V3 = f(v + (h/2)*V2)
    V4 = f(v + h*V3)
    RK4 = v + (h/6)*(V1 + 2*V2 + 2*V3 + V4)
  end function RK4
  
  function f(v)
    double precision :: v(D), f(D)
    f(1) = sigma*(v(2)-v(1))
    f(2) = v(1)*(rho-v(3))-v(2)
    f(3) = v(1)*v(2) - beta*v(3)
  end function f
end program LorenzBifurcation

Next, the following MATLAB code utilizes the OUTPUT.csv file generated above to plot the bifurcation diagram.

[file,path] = uigetfile('*.csv');
data = csvread([path,file]);
 
sz = 0.6;
scatter(data(:,1),data(:,2),sz,'.');

Julia

Below is the code to find the Lorenz attractor and plot the graph using Julia.

using DifferentialEquations
using Plots

function parameterized_lorenz!(du,u,p,t)
    x,y,z = u
    σ,ρ,β = p
    du[1] = dx = σ*(y-x)
    du[2] = dy = x*(ρ-z) - y
    du[3] = dz = x*y - β*z
end
u0 = [1.0,0.0,0.0]
tspan = (0.0,100.0)
p = [10.0,28.0,8/3]
prob = ODEProblem(parameterized_lorenz!,u0,tspan,p)
solution = solve(prob)
plot(solution, vars = (1,2,3))

Below is the code to plot the bifurcation diagram.

using DataFrames, CSV, Plots

function RK4(f::Function, v::AbstractVector, h=10^(-2))
    V1 = f(v)
    V2 = f(v + (h/2)*V1)
    V3 = f(v + (h/2)*V2)
    V4 = f(v + h*V3)
    return v + (h/6)*(V1 + 2V2 + 2V3 + V4), V1
end

function factory_lorenz(idx::Int64, ρ::Number; ic = [10.,10.,10.], tspan = [0., 10.])
    σ = 10
    β = 8/3
    function lorenz(v::AbstractVector)
        x, y, z = v
        dx = σ*(y - x)
        dy = x*(ρ - z) - y
        dz = x*y - β*z
        return [dx, dy, dz]
    end

    dt = 10^(-3)
    t_ = first(tspan):dt:last(tspan)
    
    ndatapoints = count(first(tspan) .< t_ .≤ last(tspan))
    len_t_ = length(t_)

    v = ic; DIM = length(v)
    traj = zeros(2DIM, len_t_+1)
    traj[1:DIM, 1] = v

    for tk in eachindex(t_)
        v, dv = RK4(lorenz, v, dt)
        if tk+1 ≥ (len_t_ - ndatapoints)
            traj[        1:DIM , tk+1] =  v
            traj[DIM .+ (1:DIM), tk  ] = dv
        end
    end
    traj = traj[:, 1:(end-1)]'
    traj = traj[(end-ndatapoints):end, :]

    return traj
end
factory_lorenz(T::Type, args...; ic = [10,10,10.], tspan = [0., 100.]) =
DataFrame(factory_lorenz(args...; ic = ic, tspan), ["x", "y", "z", "dx", "dy", "dz"])

r_range = 25:0.1:325
schedules = DataFrame(idx = eachindex(r_range), r = r_range)
CSV.write("G:/DDM/lyapunov/lorenz_schedules.csv", schedules)
# schedules = CSV.read("G:/DDM/lyapunov/lorenz_schedules.csv", DataFrame)
@showprogress @threads for dr in eachrow(schedules)
    data = factory_lorenz(DataFrame, dr.idx, dr.r, tspan = [0, 100])[90000:end, :]
    CSV.write("G:/DDM/lyapunov/lorenz/$(lpad(dr.idx, 5, '0')).csv", data)
end

idcs = Int64[]; vrtc = Float64[]; hrzn = Float64[]
@showprogress for dr = eachrow(schedules)
    filename = "G:/DDM/lyapunov/lorenz/$(lpad(dr.idx, 5, '0')).csv"
    !isfile(filename) && continue

    data = CSV.read(filename, DataFrame)
    idx_sampled = findall((circshift(data.z, 1) .< data.z) .&& (circshift(data.z, -1) .< data.z))[2:(end-1)]
    sampledz = data.z[idx_sampled]
    append!(idcs, fill(dr.idx, length(sampledz)))
    append!(hrzn, fill(dr.r, length(sampledz)))
    append!(vrtc, sampledz)
end
CSV.write("G:/DDM/lyapunov/lorenz_bifurcation.csv", DataFrame(; vrtc, hrzn))
scatter(hrzn, vrtc, color = :black, ms = 1, legend = :none, msw = 0, ma = 0.1, xticks = [25, 325], size = [800, 800], xlabel = L"\rho");
png("G:/DDM/lyapunov/lorenz_bifurcation.png")

Next is the code to calculate the Lyapunov exponent.

using CSV, DataFrames, LinearAlgebra, ProgressMeter, Plots, Dates; @info now()
using Base.Threads: @threads # Base.Threads.nthreads()

function RK4(f::Function, v::AbstractVector, h=1e-3)
    V1 = f(v)
    V2 = f(v + (h/2)*V1)
    V3 = f(v + (h/2)*V2)
    V4 = f(v + h*V3)
    return v + (h/6)*(V1 + 2V2 + 2V3 + V4), V1
end
function RK4(J::AbstractMatrix, U::AbstractMatrix, dt=1e-3)
    V1 = J*U
    V2 = J*(U + (dt/2)*V1)
    V3 = J*(U + (dt/2)*V2)
    V4 = J*(U + dt*V3)
    return U + (dt/6)*(V1 + 2V2 + 2V3 + V4)
end
function factory_lorenz(ρ::Number; ic = [10.,10.,10.], tspan = [0., 1000.], dt = 1e-3)
    σ = 10
    β = 8/3
    function sys(v::AbstractVector)
        x, y, z = v
        dx = σ*(y - x)
        dy = x*(ρ - z) - y
        dz = x*y - β*z
        return [dx, dy, dz]
    end
        
    t_ = first(tspan):dt:last(tspan)
    len_t_ = length(t_)
    
    t, tk = .0, 0
    v = ic; DIM = length(v)
    traj = zeros(len_t_+2, 2DIM)
    while tk ≤ len_t_
        v, dv = RK4(sys, v, dt)

        if t ≥ first(t_)
            tk += 1
            traj[tk+1,         1:DIM ] =  v
            traj[tk  , DIM .+ (1:DIM)] = dv
        end
    end
    return traj[2:(end-2), :]
end
factory_lorenz(T::Type, args...; kargs...) =
DataFrame(factory_lorenz(args...; kargs...), ["x", "y", "z", "dx", "dy", "dz"])

function gram_schmidt(J)
    N = size(J, 1)
    U, V = deepcopy(J), deepcopy(J)
    U[:,1] = V[:,1] / norm(V[:,1])
    for j in 2:N
        for jp in 1:(j-1)
            V[:,j] -= (J[:,j]'U[:,jp])*U[:,jp]
        end
        U[:,j] = V[:,j] / norm(V[:,j])
    end
    return U, V
end
J_lorenz(x,y,z,ρ) = [
     -10   10  0
      ρ-z -1  -x
        y  x  -8/3
]

const dt = 1e-3
ρ_range = 0:.1:100
cd("G:/DDM")

function lyapunov_lorenz_GS()
    schedules = DataFrame(idx = eachindex(ρ_range), ρ = ρ_range)
    schedules[!, :λ1] .= .0; schedules[!, :λ2] .= .0; schedules[!, :λ3] .= .0; 
    @showprogress @threads for dr = eachrow(schedules)
        data = factory_lorenz(DataFrame, dr.ρ; dt)
        
        λ = zeros(3);
        J = J_lorenz(collect(data[1, 1:3])..., dr.ρ)
        U = I(3)
        for i in 2:nrow(data)
            U, V = gram_schmidt(U)
            λ += V |> eachcol .|> norm .|> log          

            U = RK4(J, U, dt)
            J = J_lorenz(collect(data[i, 1:3])..., dr.ρ)
        end

        λ ./= dt*nrow(data)
        dr[[:λ1, :λ2, :λ3]] .= sort(λ, rev = true)
    end
    sort!(schedules, :ρ)
    CSV.write("lyapunov/lorenzGS.csv", schedules, bom = true)
    plot(xticks = 0:20:100, legend = :none, xlabel = "ρ", ylabel = "λ", size = [600, 300])
    plot!(schedules.ρ, schedules.λ1, lw = 2, color = 1)
    plot!(schedules.ρ, schedules.λ2, lw = 2, color = 2)
    plot!(schedules.ρ, schedules.λ3, lw = 2, color = 3)
    png("lyapunov/lorenzGS.png")
end

lyapunov_lorenz_GS()