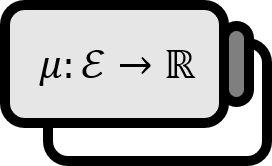Lebesgue Integrable

Definition ¹

[1]: An integrable function is a measurable function.
[2]: If $f \in \mathcal{L}^{1} (E)$ then $\displaystyle \left| \int_{E} f dm \right| \le \int_{E} | f | dm$
[3]: If $f \in \mathcal{L}^{1} (E) $ and $c \in \mathbb{R}$ then $\displaystyle \int_{E} (c f) dm = c \int_{E} f dm$
[4]: If $f,g \in \mathcal{L}^{1} (E) $ then $\displaystyle \int_{E} ( f + g ) dm = \int_{E} f dm + \int_{E} g dm$
[5]: If $f,g \in \mathcal{L}^{1} (E)$ and $f \le g$ then $\displaystyle \int_{E} f dm \le \int_{E} g dm$
[6]: For all $E \in \mathcal{M}$, if $\displaystyle \int_{E} f dm = \int_{E} g dm$ then almost everywhere $f= g$.

It might seem easy that Property [1] is directly under the definition, but it can get confusing after a while so make sure to memorize it well.

Meanwhile, from properties [3]~[5], it can be seen that $\mathcal{L}^{1}(E)$ is a vector space.

Capinski. (1999). Measure, Integral and Probability: p86. When we say $E \in \mathcal{M}$, for a measurable function $f$, let’s denote it as $$f^{+} := \max \left\{ f , 0 \right\} \\ f^{-} := \max \left\{ -f , 0 \right\}$$ Then, it can be represented as $$ f = f^{+} - f^{-} \\ | f | = f^{+} + f^{-} $$ If $\displaystyle \int_{E} | f | dm < \infty$, that is, $$ \int_{E} f^{+} dm < \infty \\ \int_{E} f^{-} dm < \infty $$ then $f$ is called Lesbegue Integrable. The set of integrable functions from $E$ is denoted as follows. $$ \mathcal{L}^{1}(E) : = \left\{ f \ \left| \ \int_{E} | f | dm < \infty \right. \right\} $$ ↩︎