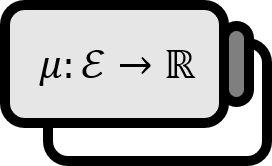Empty Set
Definition 1
For a set of real number intervals $\mathcal{I}$, define function $l : \mathcal{I} \to [ 0 , \infty )$ as $l( I ) := \sup{I} - \inf{I}$ and call it Length. If there exists a sequence of intervals $\left\{ I_{n} \ | \ n \in \mathbb{N} \right\}$ that satisfies $$ A \subset \bigcup_{n = 1}^{\infty} I_{n} \\ \sum_{n=1}^{\infty} l (I_{n}) < \varepsilon $$ for any $\varepsilon > 0$, then $A \subset \mathbb{R}$ is called a Null Set.
Capinski. (1999). Measure, Integral and Probability: p16. ↩︎