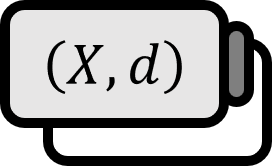Compactness in Metric Space
Definition
Open Cover
Given a metric space $(X,d)$ and a subset $E\subset X$, a set of open sets $\left\{ O_{\alpha} \right\}$ that satisfies the following equation $X$ is called an open cover of $E$.
$$ E\subset \bigcup _{\alpha} O_{\alpha} $$
A subset of an open cover is called a subcover. Specifically, a subcover with a finite number of elements is called a finite subcover.
Compact
Given a subset $K$ of a metric space $X$, if every open cover of $K$ has a finite subcover, then $K$ is said to be compact. In other words, if a finite number of elements from an open cover still form an open cover, then $K$ is considered compact. Mathematically, if for some $\alpha_{1},\cdots ,\alpha_{n}$
$$ K\subset O_{\alpha_{1}}\cup \cdots O_{\alpha_{n}} $$
then $K$ is compact.
Explanation
The importance of compactness lies in the fact that whether a set retains or loses its compactness depends on what the entire space is considered to be. In other words, compactness is an inherent property of the set. Without going far, just by looking at the concept of openness, there is no guarantee that the property of being open is preserved when the entire space is extended, hence there is the term relatively open. As one continues to study, it becomes clear that the condition of being compact plays a crucial role in various theorems. Compactness is a property that is bestowed upon a set regardless of the entire space, as can be seen in the theorem below. For now, we use the expression that $K$ is compact in the entire space $X$.
Theorem
For two metric spaces $X$, $Y$, let $K\subset Y \subset X$. Then the following two propositions are equivalent.
(a) $K$ is compact in $X$.
(b) $K$ is compact in $Y$.
Proof
Given two metric spaces $X$, $Y$, and let $E \subset Y \subset X$. Then the following two propositions are equivalent. $(d)$ $E$ is relatively open with respect to $Y$.$(e)$ For some open set $O_{X}$ in $X$, $E=Y \cap O_{X}$ holds.
(a) $\Longrightarrow$ (b)
Assume $K$ is compact in $X$. Let $\left\{ O_{\alpha}^{Y} \right\}$ be a set of open sets in $Y$ that satisfies $K\subset \bigcup_{\alpha} O_{\alpha}^{Y}$. In other words, assume $\left\{ O_{\alpha}^{Y} \right\}$ is an arbitrary open cover of $K$ with respect to $Y$. Then, by the lemma,
$$ O_{\alpha}^{Y}=Y\cap O_{\alpha}^{X},\quad \forall \alpha $$
there exists an open set $O_{\alpha}^{X}$ in $X$ that satisfies. Then, $\left\{ O_{\alpha}^{X} \right\}$ becomes an open cover of $K$ with respect to $X$. By assumption, for some $\alpha_{1},\cdots,\alpha_{n}$, the following equation holds:
$$ K \subset O_{\alpha_{1}}^{X}\cup\cdots \cup O_{\alpha_{n}}^{X} $$
But since $K\subset Y$, it follows that:
$$ \begin{align*} K & \subset Y \cap (O_{\alpha_{1}}^{X}\cup\cdots \cup O_{\alpha_{n}}^{X}) \\ &= (Y \cap O _{\alpha_{1}}^{X})\cup\cdots \cup(Y \cap O_{\alpha_{n}}^{X}) \\ &= O_{\alpha_{1}}^{Y}\cup\cdots \cup O_{\alpha_{n}}^{Y} \end{align*} $$
Therefore, since an arbitrary open cover $\left\{ O_{\alpha}^{Y} \right\}$ of $K$ with respect to $Y$ has a finite subcover that satisfies
$$ K \subset O_{\alpha_{1}}^{Y}\cup\cdots \cup O_{\alpha_{n}}^{Y} $$
$K$ is compact in $Y$.
(a) $\Longleftarrow$ (b)
Assume $K$ is compact in $Y$. Let $\left\{ O_{\alpha}^{X} \right\}$ be a set of open sets in $X$ that satisfies $K\subset \bigcup_{\alpha} O_{\alpha}^{X}$. In other words, take $K$’s arbitrary open cover with respect to $X$ as $\left\{ O_{\alpha}^{X} \right\}$. And let $O_{\alpha}^{Y}$ as follows:
$$ O_{\alpha}^{Y}=Y\cap O_{\alpha}^{X},\quad \forall \alpha $$
Then, by the lemma, $O_{\alpha}^{Y}$ becomes an open set in $Y$. Therefore, $\left\{ O_{\alpha}^{Y} \right\}$ is an open cover of $K$. By assumption, for some $\alpha_{1},\cdots,\alpha_{n}$, the following equation holds:
$$ K \subset O_{\alpha_{1}}^{Y}\cup \cdots \cup O_{\alpha_{n}}^{Y} $$
But since for each $\alpha$, $O_{\alpha}^{Y} \subset O_{\alpha}^{X}$ holds, it follows that:
$$ K\subset O_{\alpha_{1}}^{X}\cup \cdots \cup O_{\alpha_{n}}^{X} $$
Therefore, since any arbitrary open cover always has a finite subcover, $K$ is compact in $X$.
■