르벡 측도
정의 1
$E \in \mathcal{M}$ 에 대해 함수 $m : \mathcal{M} \to [0,\infty]$ 을 $m(E) := m^{ \ast } (E)$ 과 같이 정의하자. $m$ 을 (르벡) 측도라 한다.
설명
외측도는 $m^{ \ast } : \mathscr{P}( \mathbb{R} ) \to [0, \infty]$ 으로 깔끔하게 정의된 대신 길이의 일반화로써는 아쉬운 점이 있었다. 대신 실수의 시그마-필드로 정의역에 제한을 주는 것으로 이상적인 ‘길이의 일반화’를 완성했다. 이는 카라테오도리 조건을 만족시키기 위해 조건상으로 한발짝 물러난 것으로 볼 수 있다.
물론 일반적인 측도와 비교해보면 $X = \mathbb{R}$ 에서의 특수한 예긴 하다.
기초 성질
$A, B, E \in \mathcal{M}$ 이고 모든 $n \in \mathbb{N}$ 에 대해 $A_{n}, B_{n}, \in \mathcal{M}$ 이라 하자. 측도는 아래의 성질들을 가진다.
- [1]: $$A \subset B \implies m(A) \le m(B)$$
- [2]: 만약 $A \subset B$ 면, $$m(A) < \infty \implies m(B \setminus A) = m(B) - m(A)$$
- [3]: $$t \in \mathbb{R} \implies m(E) = m(E + t)$$
- [4]: $$m(A \triangle B) = 0 \implies B \in \mathcal{M} \\ m(A) = m(B)$$
- [5]: 모든 $\varepsilon > 0, A \subset \mathbb{R}$ 에 대해 다음을 만족하는 열린 $O$ 가 존재한다. $$ A \subset O \\ m(O) \le m^{ \ast }(A) + \varepsilon $$
- [6]: 모든 $A \subset \mathbb{R}$ 에 대해 다음을 만족하는 열린 집합의 수열 $\left\{ O_{n} \right\}$ 이 존재한다. $$ A \subset \bigcap_{n} O_{n} \\ m \left( \bigcap_{n} O_{n} \right) = m^{ \ast }(A) $$
- [7]: $$\displaystyle A_{n} \subset A_{n+1} \implies m \left( \bigcup_{n=1}^{\infty} A_{n} \right) = \lim_{n \to \infty} m (A_{n})$$
- [8]: 만약 $A_{n+1} \subset A_{n}$ 면, $$\displaystyle m(A_{1}) < \infty \implies m \left( \bigcap_{n=1}^{\infty} A_{n} \right) = \lim_{n \to \infty} m (A_{n})$$
- [9]: $$\displaystyle m \left( \bigsqcup_{i=1}^{n} A_{i} \right) = \sum_{i = 1}^{n} m (A_{i})$$
- [10]: $m$ 은 $\emptyset$ 에서 연속이다.
- [11]: $$B_{n} \to \emptyset \implies m(B_{n}) \to 0$$
- $A \triangle B = ( A \setminus B ) \cup ( B \setminus A )$ 이다.
증명
[1]
$m = m^{ \ast } |_{\mathcal{M}}$ 이므로 외측도의 성질에서 자연스럽게 유도된다.
■
[2]
우선 $(B \setminus A) \in \mathcal{M}$ 을 증명할 필요가 있다. $(B \setminus A) = B \cap (\mathbb{R} \setminus A) = B \cap A^{c}$ 인데 $A \in \mathcal{M}$ 이므로 $A^{c} \in \mathcal{M}$ 다. 따라서 $(B \setminus A) \in \mathcal{M}$ 이고, $(B \setminus A ) \cap A = \emptyset$ 이고 $(B \setminus A ) \cup A = B$ 이므로 $m(B \setminus A ) + m(A) = m(B)$ 이다. 가정에서 $m(A) < \infty$ 였으므로 이항하면 $m(B \setminus A) = m(B) - m(A)$ 를 얻는다.
■
[3]
$m = m^{ \ast } |_{\mathcal{M}}$ 이므로 외측도의 성질에서 자연스럽게 유도된다.
■
[4]
$B = (A \cap B) \cup (B \setminus A) = A \setminus (A \setminus B) \cup (B \setminus A)$ 이므로 $B \in \mathcal{M}$ 이다. 한편 $m(A \triangle B) = 0$ 이므로 $m(A \setminus B) = 0$ 그리고 $m(B \setminus A) = 0$ 이다. 따라서 $$ m(B) = m( B \setminus A) + m(B \cap A) = m( A \setminus B) + m(A \cap B) = m(A) $$
■
[7]
$B_{n} :=A_{n} \setminus A_{n-1}$ 이라고 하면 $i \ne j$ 에 대해 $B_{i} \cap B_{j} = \emptyset$ 이고 $\displaystyle \bigcup_{n=1}^{\infty} A_{n} = \bigsqcup_{n=1}^{\infty} B_{n}$ 이다. 따라서 $$ m \left( \bigcup_{n=1}^{\infty} A_{n} \right) = m \left( \bigsqcup_{n=1}^{\infty} B_{n} \right) = \sum_{n=1}^{\infty} m(B_{n}) = \lim_{n \to \infty} \sum_{k=1}^{n} m(B_{k}) = \lim_{n \to \infty} m \left( \bigsqcup_{k=1}^{n} B_{k} \right) = \lim_{n \to \infty} m \left( A_{n} \right) $$
■
[8]
$(A_{1} \setminus A_{n} ) \subset (A_{1} \setminus A_{n+1} )$ 이므로 [7] 에 의해 $$ m \left( \bigcup_{n=1}^{\infty} ( A_{1} \setminus A_{n} ) \right) = \lim_{ n \to \infty} m (A_{1} \setminus A_{n}) $$ $m(A_{n}) < \infty$ 이므로 [3]에 의해 $$ m (A_{1} \setminus A_{n}) = m(A_{1}) - m(A_{n}) $$ 한편 $\displaystyle \bigcup_{n=1}^{\infty} (A_{1} \setminus A_{n}) = A_{1} \setminus \bigcap_{n=1}^{\infty} A_{n}$ 이므로 $$ m \left( \bigcup_{n=1}^{\infty} (A_{1} \setminus A_{n}) \right) = m \left( A_{1} \right) - m \left( \bigcap_{n=1}^{\infty} A_{n} \right) $$ 정리하면 $$ m \left( \bigcup_{n=1}^{\infty} (A_{1} \setminus A_{n}) \right) = m(A_{1}) - \lim_{n \to \infty} m(A_{n}) = m \left( A_{1} \right) - m \left( \bigcap_{n=1}^{\infty} A_{n} \right) $$ 따라서 $\displaystyle \lim_{n \to \infty} m(A_{n}) = m \left( \bigcap_{n=1}^{\infty} A_{n} \right)$
■
일반화
Capinski. (1999). Measure, Integral and Probability: p35. ↩︎
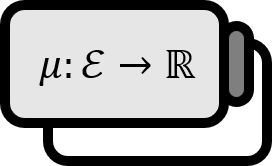
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

