📂힐베르트공간

자기 수반 작용소

정의

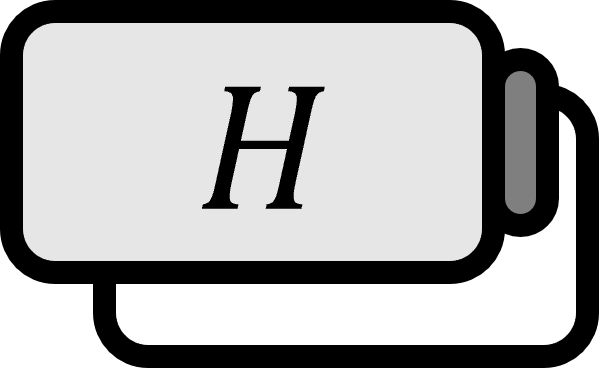
힐베르트 공간 $H$와 유계 선형 작용소 $T : H \to H$가 다음을 만족하면 자기수반 작용소^{self-adjoint operator}라 한다.

$$ T^{\ast} = T $$

$T^{\ast}$는 $T$의 수반 작용소이다.

설명

자기수반이면, 정규작용소$(T^{\ast}T = TT^{\ast})$이다. 정의의 조건을 다르게 쓰면 아래와 같다.

$$ \braket{T \mathbf{x}, \mathbf{y}} = \braket{\mathbf{x}, T \mathbf{y}}, \qquad \forall \mathbf{x}, \mathbf{y} \in H $$

유한차원에서는, 즉 행렬로 보면 $T^{\ast}$는 $T$의 켤레 전치행렬이고 $T^{\ast} = T$인 $T$를 에르미트행렬이라 한다. 즉 자기수반 작용소는 에르미트 행렬의 일반화이다.

성질¹

$H$를 힐베르트공간, $T, S : H \to H$를 유계 선형 작용소라고 하자. 그러면 다음이 성립한다.

(a) $T$가 자기수반이면, 모든 $x \in H$에 대해서 $\braket{T\mathbf{x}, \mathbf{x}}$는 실수^real이다.

(b) $H$가 복소벡터공간이고 모든 $x \in H$에 대해서 $\braket{T \mathbf{x}, \mathbf{x}}$가 실수이면, $T$는 자기수반이다.

(c) 두 자기수반 작용소 $S$와 $T$에 대해서, $ST$가 자기수반인 것은, $S$와 $T$가 서로 교환가능한 것과 동치이다. $$ ST \text{ is self-adjoint} \iff ST = TS \text{ (for self-adjoint $S$ and $T$)} $$

(d) 임의의 유계선형작용소 $T : H \to H$와 이의 수반작용소는 두 자기수반작용소 $T_{1}$과 $T_{2}$의 선형결합으로 유일하게 표현된다. $$ T = T_{1} + iT_{2}, \qquad T^{\ast} = T_{1} - iT_{2} $$ 이때 $T_{1}$과 $T_{2}$는 각각 다음과 같다. $$ T_{1} = \frac{1}{2}(T + T^{\ast}), \qquad T_{2} = \frac{1}{2i}(T - T^{\ast}) $$

증명

(a)

$T$가 자기수반이라고 하자. 내적의 정의와 자기수반의 정의에 의해 다음이 성립한다.

$$ \overline{\braket{T \mathbf{x}, \mathbf{x}}} = \braket{\mathbf{x}, T \mathbf{x}} = \braket{T \mathbf{x}, \mathbf{x}}, \quad \forall \mathbf{x} \in H $$

따라서 $\braket{T \mathbf{x}, \mathbf{x}}$는 실수이다.

■

(b)

실수는 켤레전치를 씌워도 값이 같으므로, 수반작용소와 내적의 정의에 의해 다음이 성립한다.

$$ \braket{T \mathbf{x}, \mathbf{x}} = \overline{\braket{T \mathbf{x}, \mathbf{x}}} = \overline{\braket{\mathbf{x}, T^{\ast} \mathbf{x}}} = \braket{T^{\ast} \mathbf{x}, \mathbf{x}}, \quad \forall \mathbf{x} \in H $$

그러면 다음을 얻는다.

$$ \braket{T \mathbf{x}, \mathbf{x}} - \braket{T^{\ast} \mathbf{x}, \mathbf{x}} = \braket{(T - T^{\ast}) \mathbf{x}, \mathbf{x}} = 0, \quad \forall \mathbf{x} \in H $$

영 작용소의 성질

복소벡터공간 $X$에 대해서, $Q : X \to X$가 모든 $x \in X$에 대해서 $\braket{Qx, x} = 0$이면, $Q = 0_{\text{op}}$이다.

그러면 영 작용소의 성질에 의해 다음이 성립하고, $T$는 자기수반이다.

$$ T - T^{\ast} = 0 \implies T = T^{\ast} $$

■

(c)

곱의 수반작용소는 $(ST)^{\ast} = T^{\ast}S^{\ast}$인데, 두 작용소를 자기수반이라 가정했으므로 다음을 얻는다.

$$ (ST)^{\ast} = TS \tag{1} $$

$(\implies)$ $ST$가 자기수반이라고 하자. 그러면 다음이 성립한다.

$$ (ST)^{\ast} = ST \tag{2} $$

$(1)$과 $(2)$에 의해 $TS = ST$가 성립한다.

■

$(\impliedby)$ $ST = TS$라고 하자. 그러면 $(1)$에 의해 다음이 성립한다.

$$ (ST)^{\ast} = TS = ST \implies (ST)^{\ast} = ST $$

따라서 $ST$는 자기수반이다.

■

(d)

우선 $T_{1} = \frac{1}{2}(T + T^{\ast})$과 $T_{2} = \frac{1}{2i}(T - T^{\ast})$가 자기수반인 것은 쉽게 알 수 있다.

$$ \begin{align*} \Braket{\frac{1}{2}(T + T^{\ast})x, y} &= \Braket{x, \left[ \frac{1}{2}(T + T^{\ast}) \right]^{\ast}y} \\ &= \Braket{x, \frac{1}{2}(T^{\ast} + T)y} \\ &= \Braket{x, \frac{1}{2}(T + T^{\ast})y} \end{align*} $$

그리고,

$$ \begin{align*} \Braket{\frac{1}{2i}(T - T^{\ast})x, y} &= \Braket{x, \left[ \frac{1}{2i}(T - T^{\ast}) \right]^{\ast}y} \\ &= \Braket{x, \overline{\frac{1}{2i}}(T^{\ast} - T)y} \\ &= \Braket{x, \frac{1}{2i}(-T^{\ast} + T)y} \\ &= \Braket{x, \frac{1}{2i}(T - T^{\ast})y} \end{align*} $$

$T = T_{1} + iT_{2}$, $T^{\ast} = T_{1} - iT_{2}$인 것은 자명하다.

■