측도론에서의 거의 어디서나와 거의 확실히
정의 1
함수 $f : E \to \overline{\mathbb{R}}$ 가 $m(E_{0}) = 0$ 인 $E_{0} \subset E$ 을 제외하고 어떤 성질 $P$ 를 가질 때, $f$ 는 $E$ 의 거의 어디서나 $P$ 를 가진다고 한다.
표기
확률을 이야기 할 때 거의 어디서나almost Everywhere는 거의 확실히almost Surely 로 표현하며, 한국어만으로 표기하는 게 번거로울 때는 다음과 같이 약자를 써서 표현한다. $$ f = g \text{ a.e.} \\ P(E) = 0 \text{ a.s.} $$
설명
쉽게 말하면 영집합을 제외한 모든 점을 ‘거의 모든 곳’으로 보는 것이다. 이러한 개념은 새삼 정의해서 생소할 뿐 고등학교에서 정적분을 배울 때 이미 알고 있던 것이다. 때문에 위끝과 아래끝이 같으면 그 정적분은 반드시 $0$ 이었고, 확률을 계산할 때도 끝 점이 포함되느냐, 포함되지 않느냐는 무시했다.
기초 성질
- [1]: $f : E \to \mathbb{R}$ 가 가측이고 $E$ 의 거의 어디서나 $f = g$ 면 $g$ 는 $E$ 에서 가측이다.
- [2]: $f,g$ 가 $E$ 에서 가측이고 $E$ 의 거의 어디서나 $|f| , |g| < \infty$ 면 $\alpha f + \beta g$ 는 $E$ 에서 가측이다.
- [3]: $f,g$ 가 $E$ 에서 가측이고 $E$ 의 거의 어디서나 $|f| , |g| < \infty$ 면 $f g$ 는 가측이다.
증명
이 성질들은 한번 정도는 손으로 직접 증명해보는 게 좋긴 한데, 증명하는 재미만 생각해보면 [3] 외에는 그다지 볼만한 게 없다.
[1]
$E_{0} = \left\{ x \in E \ | \ f(x) \ne g(x) \right\}$ 라고 하면 $E_{0} \subset E$ 고 $m(E_{0}) = 0$ 이다. 임의의 $c$ 에 대해 $$ \left\{ x \in E \ | \ g(x) > c \right\} = \left\{ x \in E_{0} \ | \ g(x) > c \right\} \cup \left[ \left\{ x \in E \ | \ f(x) > c \right\} \cap ( E \setminus E_{0} ) \right] $$ 라고 하자. 우변의 항을 하나씩 살펴보면 $\left\{ x \in E_{0} \ | \ g(x) > c \right\} \subset E_{0}$ 이므로 $$ \left\{ x \in E_{0} \ | \ g(x) > c \right\} \in \mathcal{M} $$ $f$ 는 $E$ 에서 가측이므로 $$ \left\{ x \in E \ | \ f(x) > c \right\} \in \mathcal{M} $$ 마지막으로 $$ E \cap (\mathbb{R} \setminus E_{0}) = ( E \setminus E_{0} ) \in \mathcal{M} $$ 따라서 $\left\{ x \in E \ | \ g(x) > c \right\} \in \mathcal{M}$ 이고, $g$ 는 $E$ 에서 가측이다.
■
[2]
$\alpha = 0$ 이면 $\alpha f$ 는 가측이고 $\beta = 0$ 이면 $\beta g $ 는 가측이다.
$\alpha \ne 0$ 이면 $f$ 가 가측이므로 임의의 $\displaystyle {{c} \over {\alpha}}$ 에 대해 $$ \left\{ x \in E \ \left| \ f(x) > {{c} \over {\alpha}} \right. \right\} \in \mathcal{M} $$ 여기서 $\alpha> 0$ 면 $$ \left\{ x \in E \ | \ \alpha f(x) > c \right\} \in \mathcal{M} $$ 이고 $\alpha <0$ 면 $$ \left\{ x \in E \ | \ \alpha f(x) < c \right\} \in \mathcal{M} $$ 따라서 $\alpha f$ 는 가측이고, 같은 방법으로 $\beta \ne 0$ 일 때 $\beta g$ 가 가측이라는 것도 같은 방법으로 보일 수 있다.
이제 $(f + g)$ 가 가측, 즉 $\left\{ x \in E \ | \ f(x) + g(x) < c \right\} \in \mathcal{M}$ 을 보이면 증명은 끝난다. 두 함수는 유한한 값을 가지므로 모든 $x \in E$ 에 대해 $f(x) + g(x) < c$ 를 만족하는 $c \in \mathbb{R}$ 가 존재할 것이다. 다시 나타내면 $f(x) < c - g(x)$ 고 유리수의 조밀성에 의해 $f(x) < q < c - g(x)$ 를 만족하는 $q \in \mathbb{Q}$ 가 존재한다. 그러면 $$ \bigcup_{q \in \mathbb{Q}} \left\{ x \in E \ | \ g(x) < c - q \right\} \cap \left\{ x \in \ | \ E f(x) < q \right\} = \left\{ x \in E \ | \ f(x) + g(x) < c \right\} \in \mathcal{M} $$
■
Strategy[3]**: $fg$ 가 가측임을 보이는 아이디어는 $\displaystyle fg = {{1} \over {2}} \left[ (f+ g)^2 - f^2 - g^2\right]$ 이 등식 하나로 요약된다.
[3]
이미 [2]에서 함숫값이 발산하지 않는 가측 함수들의 합은 가측임을 보였으므로, $f^2$ 이 가측임을 보이면 충분하다. $f$ 는 가측이므로 모든 $c$ 에 대해 $$ \left\{ x \in E \ | \ f(x) > \sqrt{c} \right\} \in \mathcal{M} \\ \left\{ x \in E \ | \ f(x) < - \sqrt{c} \right\} \in \mathcal{M} $$ 이다. 따라서 $$ \left\{ x \in E \ | \ f(x) > \sqrt{c} \right\} \cup \left\{ x \in E \ | \ f(x) < - \sqrt{c} \right\} = \left\{ x \in E \ | \ f^2 (x) > c \right\} \in \mathcal{M} $$
■
같이보기
Capinski. (1999). Measure, Integral and Probability: p55. ↩︎
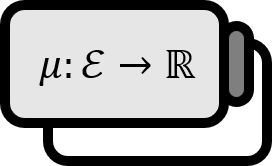
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

