3차원 데카르트 좌표계에서 벡터 함수의 컬(회전)
정의
벡터 함수 $\mathbf{F}(x,y,z)=(F_{x},F_{y},F_{z})=F_{x}\hat{\mathbf{x}} + F_{y}\hat{\mathbf{y}} + F_{z}\hat{\mathbf{z}}$에 대해서 다음과 같은 벡터를 $\mathbf{F}$의 컬curl이라 정의하고 $\nabla \times \mathbf{F}$라고 표기한다.
$$ \begin{align} \nabla \times \mathbf{F} &= \left( \dfrac{ \partial F_{z}}{ \partial y }-\dfrac{ \partial F_{y}}{ \partial z} \right)\hat{\mathbf{x}}+ \left( \dfrac{ \partial F_{x}}{ \partial z }-\dfrac{ \partial F_{z}}{ \partial x} \right)\hat{\mathbf{y}}+ \left( \dfrac{ \partial F_{y}}{ \partial x }-\dfrac{ \partial F_{x}}{ \partial y} \right)\hat{\mathbf{z}} \label{def1} \\ &=\begin{vmatrix} \hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \\ \dfrac{ \partial }{ \partial x} & \dfrac{ \partial }{ \partial y } & \dfrac{ \partial }{ \partial z} \\ F_{x} & F_{y} &F_{z}\end{vmatrix} \label{def2} \end{align} $$
- $(2)$는 $\mathbf{F}$의 컬을 쉽게 외우는 공식이다. 행렬식이라고 생각하고 그대로 전개하면 된다.
설명
curl은 회전으로 번역된다. 그런데 회전이라는 말은 너무 일상적이기도 하고, curl이 아니라 rotation으로 오해할 여지가 있으므로 생새우초밥집에서는 회전 대신 컬을 사용한다.
$\nabla \times \mathbf{F}$는 $\mathbf{F}$라는 물리량이 어느 방향으로 회전하고있는지는 말해주는 벡터이다. $\nabla \times \mathbf{F}$의 방향을 축(엄지)으로 두고 오른손 법칙을 적용하면 오른손이 감싸는 방향과 $\mathbf{F}$가 회전하는 방향이 같다. 벡터 $\nabla \times \mathbf{F}$의 크기는 회전하는 정도를 나타낸다.
아인슈타인 표기법과 레비-치비타 심볼을 사용하면 다음과 같이 나타낼 수 있다. $\nabla_{j} = \dfrac{\partial }{\partial x_{j}}$라고 표기하면,
$$ \nabla \times \mathbf{F} = \epsilon_{ijk}\hat{\mathbf{e}}_{i}\nabla_{j}F_{k} $$
한편 정의에서 $(1)$이라는 값을 $\nabla \times \mathbf{F}$로 표기한다고 한 것에 주의하자. $\nabla$를 델 연산자라 부르기는 하지만, 이것 자체로 어떤 의미를 가진다고 생각하면 $\nabla \cdot \mathbf{F}$나 $\nabla \times \mathbf{F}$를 내적과 외적으로 오해하기 딱 좋다. 따라서 $\nabla$는 그저 편리한 표기법 정도로만 이해해야하며, 그래디언트, 다이벌전스, 컬을 묶어 델 연산자들이라고 부른다고 하거나, 차라리 델 연산자=그래디언트라고 생각하는게 더 나을 수 있다. 자세한 내용은 아래에서 이어진다.
주의할 점
$\nabla \times \mathbf{F}$는 $\nabla$와 $\mathbf{F}$의 외적이 아니다
그저 $\nabla \times \mathbf{F}$는 $\mathbf{F}$에 대한 어떤 정보를 담고 있는 벡터이다. $\nabla$를 $\nabla = \dfrac{ \partial }{ \partial x}\hat{\mathbf{x}} + \dfrac{ \partial }{ \partial y}\hat{\mathbf{y}} + \dfrac{ \partial }{ \partial z}\hat{\mathbf{z}}$과 같은 벡터라고 생각하고 계산한 결과가 $(1)$과 찰떡같이 맞아떨어지므로, 편의를 위해 $\nabla \times \mathbf{F}$와 같이 표기하는 것일 뿐이다. 만약 $\nabla$가 실제로 벡터라고 가정하면 이상한 결과를 얻는다.
두 벡터 $\mathbf{A}, \mathbf{B}$에 대해서 다음의 식이 성립한다.
$\nabla$가 정말 벡터라면 위의 공식에 대입할 수 있고, 그러면 다음의 결과를 얻는다.
$$ \nabla \times (\nabla \times \mathbf{F})=(\mathbf{F} \cdot \nabla)\nabla - (\nabla \cdot \nabla)\mathbf{F} + \nabla (\nabla \cdot \mathbf{F}) - \mathbf{F} (\nabla \cdot \nabla) $$
하지만 올바른 결과는 다음과 같다.
$$ \nabla \times (\nabla \times \mathbf{F})=\nabla(\nabla \cdot \mathbf{F})-\nabla ^{2} \mathbf{F} $$
다른 예도 있다. 벡터의 외적은 반교환성을 가지므로 $\nabla \times \mathbf{F}$가 외적이라면 다음이 식이 성립해야한다.
$$ \nabla \times \mathbf{F} \overset{?}{=} - \mathbf{F} \times \nabla $$
따라서 $\nabla$는 벡터가 아니고, $\nabla \times \mathbf{F}$를 $\nabla$와 $\mathbf{F}$의 외적이 아니라는 것을 알 수 있다. 벡터라가 아니라 $\nabla \times$ 자체를 하나의 함수라고 생각해야한다. 이와 같이 함수를 변수로갖는 함수를 물리학에선 연산자라고 한다.
그럼 $\nabla \times \mathbf{F}$와 $\mathbf{F} \times \nabla$의 차이는?
$\nabla \times$는 벡터함수를 변수로 갖는, 다음과 같이 정의되는 연산자이다.
$$ \nabla \times (\mathbf{F}) = \left( \dfrac{ \partial F_{z}}{ \partial y }-\dfrac{ \partial F_{y}}{ \partial z} \right)\hat{\mathbf{x}}+ \left( \dfrac{ \partial F_{x}}{ \partial z }-\dfrac{ \partial F_{z}}{ \partial x} \right)\hat{\mathbf{y}}+ \left( \dfrac{ \partial F_{y}}{ \partial x }-\dfrac{ \partial F_{x}}{ \partial y} \right)\hat{\mathbf{z}} $$
다시말해 $\nabla \times \mathbf{F}$는 $\nabla \times$라는 연산자(함수)에 $\mathbf{F}$라는 변수를 대입했을 때의 함숫값이다. 물론 이는 다시 $(x,y,z)$를 변수로 갖는 벡터함수이다. $\nabla \times \mathbf{F}$가 $\nabla \times$의 함숫값인 반면에, $\mathbf{F} \times \nabla$는 이 자체로 하나의 연산자이다. 자주 쓰이는 수식은 아니지만, 정의를 하자면 다음과 같은 미분 연산자라고 할 수 있다.
$$ \begin{align*} \mathbf{F} \times \nabla &= \begin{vmatrix} \hat{\mathbf{x}} & \hat{\mathbf{y}} & \hat{\mathbf{z}} \\ F_{x} & F_{y} &F_{z} \\ \dfrac{ \partial }{ \partial x} & \dfrac{ \partial }{ \partial y } & \dfrac{ \partial }{ \partial z} \end{vmatrix} \\ &= \left( F_{y}\dfrac{ \partial }{ \partial z} - F_{z}\dfrac{ \partial }{ \partial y} \right)\hat{\mathbf{x}} + \left( F_{z}\dfrac{ \partial }{ \partial x} - F_{x}\dfrac{ \partial }{ \partial z} \right)\hat{\mathbf{y}} + \left( F_{x}\dfrac{ \partial }{ \partial y} - F_{y}\dfrac{ \partial }{ \partial x} \right)\hat{\mathbf{z}} \end{align*} $$
유도
이제 회전하는 벡터함수의 회전방향(시계인지 반시계인지)을 말해주는 함수에 대해서 생각해보자. 여기서 중요한 사실은 회전면 내의 어떤 방향도 회전의 방향을 특정할 수 없다는 것이다. 아래의 그림을 보자.

- 벡터 $-\hat{\mathbf{x}}$는 점 $A$에서의 움직임은 설명할 수 있지만, $B$에서의 움직임은 설명할 수 없다.
- 벡터 $\hat{\mathbf{y}}$는 점 $C$에서의 움직임은 설명할 수 있지만, $D$에서의 움직임은 설명할 수 없다.
- 벡터 $\hat{\mathbf{x}} + \hat{\mathbf{y}}$는 경로 $F$를 설명할 수는 있지만, $G$를 설명할 수 없다.
이는 시계방향의 경우도 마찬가지다. 이제 회전방향을 특정하기 위해서 회전면을 벗어날 필요가 있음을 체감할 것이다. 사실 이를 결정하기 위한 좋은 방법이 이미 있다. 바로 오른손 법칙으로 결정하는 것인데, 오른손이 휘감는 방향의 회전 축을 엄지 방향으로 결정하는 것이다. 따라서 $xy$-평면에서 반시계방향으로 돌아가는 회전의 축(방향)은 $\hat{\mathbf{z}}$이고, 시계방향으로 돌아가는 회전의 축(방향)은 $-\hat{\mathbf{x}}$이다.
그러면 이제 $\mathbf{F}$가 $xy$-평면에서 반시계방향으로 돌아가고 있을 때 $\hat{\mathbf{z}}$ 방향을 나타내는 값, 다시말해 양수인 값을 찾아보자. 회전은 간단히 아래와 같이 사각형으로 나타내자.
경로 ①은 점 $a$에서 $b$까지 움직이고, $\mathbf{F}(a) = (1,0,0)$, $\mathbf{F}(b) = (0,1,0)$이라고 하자. 그러면 점 $a$에서 $b$까지 $x$는 $+1$만큼 변화하고, $F_{y}$도 $+1$만큼 변화하므로 다음을 얻는다.
$$ \dfrac{\partial F_{y}}{\partial x} \gt 0 $$
같은 방식으로 점이 $b$에서 $c$까지 움직이는 경로에서, $y$는 $+1$만큼 변화하고, $F_{x}$는 $-1$만큼 변화한다. 네 경로에 대해서 모두 확인해보면,
$$ \dfrac{\partial F_{y}}{\partial x} \gt 0 \quad \text{in path $\textcircled{1}$, $\textcircled{3}$} $$
$$ \dfrac{\partial F_{x}}{\partial y} \lt 0 \quad \text{in path $\textcircled{2}$, $\textcircled{4}$} $$
따라서 위와 같이 반시계 방향으로 회전하는 벡터 $\mathbf{F}$에 대해서, 아래의 값은 항상 양수이다.
$$ \dfrac{\partial F_{y}}{\partial x} - \dfrac{\partial F_{x}}{\partial y} \gt 0 $$
반대로 $\mathbf{F}$가 시계방향으로 회전하고 있다면 위의 값은 항상 음수이다. 그럼 이제 벡터함수 $\mathbf{F}$를 대입할 때 마다 $xy$-평면에서 회전하는 방향과 크기를 나타내는 연산자 $\operatorname{curl}_{xy}$을 다음과 같이 정의할 수 있다.
$$ \operatorname{curl}_{xy} (\mathbf{F}) = \left( \dfrac{\partial F_{y}}{\partial x} - \dfrac{\partial F_{x}}{\partial y} \right) \hat{\mathbf{z}} $$
- 이 함수의 $\hat{\mathbf{z}}$ 성분의 부호는 $\mathbf{F}$가 $xy$-평면에서 회전하는 방향을 나타낸다.
- $+$이면 $\mathbf{F}$는 $xy$-평면에서 반시계방향으로 회전한다.
- $-$이면 $\mathbf{F}$는 $xy-$평면에서 시계방향으로 회전한다.
- $0$이면 회전하지 않는다.
- 이 함수의 $\hat{\mathbf{z}}$ 성분의 크기는 $\mathbf{F}$가 $xy$-평면에서 얼마나 빠르게 회전하는지를 나타낸다.
이제 이와 같은 논의를 $yz$-평면과 $zx$-평면에도 적용하여, $\mathbf{F}$가 3차원 공간에서 회전하고있는 방향과 크기를 나타내는 벡터 $\nabla \times \mathbf{F}$를 다음과 같이 정의할 수 있다.
$$ \nabla \times \mathbf{F} := \left( \dfrac{\partial F_{z}}{\partial y} - \dfrac{\partial F_{y}}{\partial z} \right)\hat{\mathbf{x}} + \left( \dfrac{\partial F_{x}}{\partial z} - \dfrac{\partial F_{z}}{\partial x} \right)\hat{\mathbf{y}} + \left( \dfrac{\partial F_{y}}{\partial x} - \dfrac{\partial F_{x}}{\partial y} \right)\hat{\mathbf{z}} $$
■
관련된 공식
선형성: $$ \nabla \times (\mathbf{A} + \mathbf{B}) = \nabla \times \mathbf{A} + \nabla \times \mathbf{B} $$
$$ \nabla \times (f\mathbf{A}) = f(\nabla \times \mathbf{A}) - \mathbf{A} \times (\nabla f) $$
$$ \nabla \times (\mathbf{A} \times \mathbf{B}) = (\mathbf{B} \cdot \nabla)\mathbf{A} - (\mathbf{A} \cdot \nabla)\mathbf{B} + \mathbf{A} (\nabla \cdot \mathbf{B}) - \mathbf{B} (\nabla \cdot \mathbf{A}) $$
$$ \nabla \times (\nabla f) = \mathbf{0} $$
$$ \nabla \times (\nabla \times \mathbf{F}) = \nabla (\nabla \cdot \mathbf{F}) - \nabla^{2} \mathbf{F} $$
스토크스 정리 $$ \int_{\mathcal{S}} (\nabla \times \mathbf{v} )\cdot d\mathbf{a} = \oint_{\mathcal{P}} \mathbf{v} \cdot d\mathbf{l} $$
적분 공식 $$ \int_{\mathcal{V}} (\nabla \times \mathbf{v}) d \tau = - \oint_{\mathcal{S}} \mathbf{v} \times d \mathbf{a} $$
$$ \int_{\mathcal{S}} \nabla T \times d \mathbf{a} = - \oint_{\mathcal{P}} T d \mathbf{l} $$
부분적분 $$ \int_{\mathcal{S}} f \left( \nabla \times \mathbf{A} \right)\mathbf{A} \cdot d \mathbf{a} = \int_{\mathcal{S}} \left[ \mathbf{A} \times \left( \nabla f \right) \right] \cdot d\mathbf{a} + \oint_{\mathcal{P}} f\mathbf{A} \cdot d\mathbf{l} $$
$$ \int_{\mathcal{V}} \mathbf{B} \cdot \left( \nabla \times \mathbf{A} \right) d\tau = \int_{\mathcal{V}} \mathbf{A} \cdot \left( \nabla \times \mathbf{B} \right) d\tau + \oint_{\mathcal{S}} \left( \mathbf{A} \times \mathbf{B} \right) \cdot d \mathbf{a} $$
증명
선형성
아인슈타인 표기법, 레비-치비타 심볼을 사용한다. $\nabla_{j} = \dfrac{\partial }{\partial x_{j}}$라고 하면,
$$ \begin{align*} \left[ \nabla \times (\mathbf{A} + \mathbf{B}) \right]_{i} &= \epsilon_{ijk} \nabla_{j} (\mathbf{A} + \mathbf{B})_{k} \\ &= \epsilon_{ijk} \nabla_{j} (A_{k} + B_{k}) \\ &= \epsilon_{ijk} \nabla_{j}A_{k} + \epsilon_{ijk} \nabla_{j}B_{k} \\ &= [\nabla \times \mathbf{A}]_{i} + [\nabla \times \mathbf{B}]_{i} \\ \end{align*} $$
세번째 등호는 $\dfrac{\partial (A_{k} + B_{k})}{\partial x_{j}} = \dfrac{\partial A_{k}}{\partial x_{j}} + \dfrac{\partial B_{k}}{\partial x_{j}}$이므로 성립한다.
■
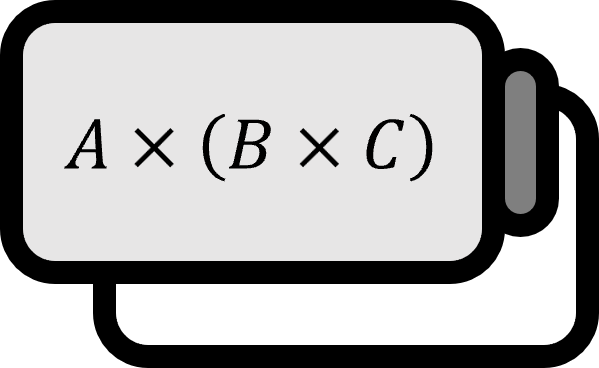
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

