힐베르트 공간에서의 베셀 시퀀스
정의1
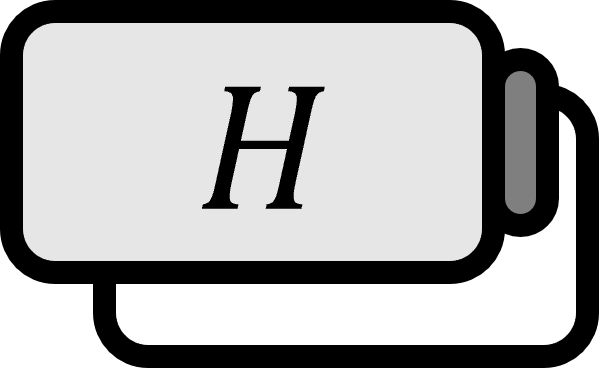
힐베르트 공간 $H$의 시퀀스 $\left\{ \mathbf{v}_{k} \right\}_{k \in \mathbb{N}} \subset H$에 대해 다음을 만족하는 $B > 0$가 존재하면 $\left\{ \mathbf{v}_{k} \right\}_{k \in \mathbb{N}}$를 베셀 시퀀스bessel sequence라 하고 $B$를 베셀 바운드bessel bound라 한다.
$$ \sum_{k=1}^{\infty} \left| \left\langle \mathbf{v} , \mathbf{v}_{k} \right\rangle \right|^{2 } \le B \left\| \mathbf{v} \right\|^{2}, \quad \forall \mathbf{v} \in H $$
설명
베셀 시퀀스는 직관적으로 봤을 때 무한차원 벡터 $\mathbf{v}$의 계수가 뒤로 갈수록 작아지도록 휘어주는 시퀀스로 볼 수 있다. 거의 대부분의 수학이 그러하듯 바운드 될 수 없는 무언가는 연구하기가 어려운데, 베셀 시퀀스의 존재성이 주어지는 것만으로도 여러가지 위험한 비약에서 자유로워질 수 있다. 물론 그 존재성을 파악하기 위해 다음과 같이 간단한 동치조건이 알려져있다.
정리
힐베르트 공간 $H$의 시퀀스 $\left\{ \mathbf{v}_{k} \right\}_{k \in \mathbb{N}} \subset H$과 $B > 0$가 주어져 있다고 하면 아래의 두 조건은 동치이다.
$\left\{ \mathbf{v}_{k} \right\}_{k \in \mathbb{N}}$가 베셀 바운드 $B$인 베셀 시퀀스다.
다음과 같이 정의된 작용소 $T$가 선형이고 유계면서 $\left\| T \right\| \le \sqrt{B}$.
$$ T : l^{2} \to H \\ T \left\{ c_{k} \right\}_{k \in \mathbb{N}} := \sum_{k \in \mathbb{N}} c_{k} \mathbf{v}_{k} $$
증명
$(\implies)$
$\left\{ \mathbf{v}_{k} \right\}_{k \in \mathbb{N}}$가 베셀 바운드 $B$인 베셀 시퀀스고 $\left\{ c_{k} \right\}_{k \in \mathbb{N}} \in l^{2}$라 하자. $T \left\{ c_{k} \right\}_{k \in \mathbb{N}} = \sum_{k \in \mathbb{N}} c_{k} \mathbf{v}_{k}$가 수렴해서 잘 정의됨을 보이기 위해 두 자연수 $n > m$ 을 생각해보면
$$ \left\| \sum_{k =1}^{n} c_{k} \mathbf{v}_{k} - \sum_{k =1}^{m} c_{k} \mathbf{v}_{k} \right\| = \left\| \sum_{k = m + 1}^{n} c_{k} \mathbf{v}_{k} \right\| = \sup_{\left\| \mathbf{w} \right\| = 1 } \left| \sum_{k = m + 1}^{n} \left\langle c_{k} \mathbf{v}_{k} , \mathbf{w} \right\rangle \right| $$
삼각 부등식에 의해
$$ \sup_{\left\| \mathbf{w} \right\| = 1 } \left| \sum_{k = m + 1}^{n} \left\langle c_{k} \mathbf{v}_{k} , \mathbf{w} \right\rangle \right| \le \sup_{\left\| \mathbf{w} \right\| = 1 } \sum_{k = m + 1}^{n} \left| \left\langle c_{k} \mathbf{v}_{k} , \mathbf{w} \right\rangle \right| $$
코시-슈바르츠 부등식에 의해
$$ \begin{align*} & \sup_{\left\| \mathbf{w} \right\| = 1 } \sum_{k = m + 1}^{n} \left| \left\langle c_{k} \mathbf{v}_{k} , \mathbf{w} \right\rangle \right| \\ \le & \left( \sum_{k = m + 1}^{n} \left| c_{k} \right|^{2} \right)^{1/2} \sup_{\left\| \mathbf{w} \right\| = 1 } \left( \sum_{k = m + 1}^{n} \left| \left\langle \mathbf{v}_{k} , \mathbf{w} \right\rangle \right|^{2} \right)^{1/2} \\ \le & \left( \sum_{k = m + 1}^{n} \left| c_{k} \right|^{2} \right)^{1/2} \sqrt{B} \end{align*} $$
$\left\{ c_{k} \right\}_{k \in \mathbb{N}} \in l^{2}$ 는 코시 수열이므로 $\displaystyle \left\{ \sum_{k=1}^{n} c_{k} \mathbf{v} \right\}_{n=1}^{\infty} \subset H$ 역시 코시 수열이고 따라서 $T$가 잘 정의됨을 확인할 수 있다. $T$는 그 정의에 따라 선형이고,
$$ \begin{align*} \left\| T \left\{ c_{K} \right\}_{k \in \mathbb{N}} \right\| =& \sup_{\left\| \mathbf{w} \right\| = 1 } \left| \left\langle T \left\{ c_{k} \right\}_{k \in \mathbb{N}} , \mathbf{w} \right\rangle \right| \\ \le & \sqrt{B} \left( \sum_{k \in \mathbb{N}} \left| c_{k} \right|^{2} \right)^{1/2} \\ =& \sqrt{B} \left\| \left\{ c_{k \in \mathbb{N}} \right\} \right\|_{2} \end{align*} $$
이므로 양변을 $\left\| \left\{ c_{k \in \mathbb{N}} \right\} \right\|_{2}$로 나누면 $\left\| T \right\| \le \sqrt{B}$를 얻는다.
$(\impliedby)$
$\left\{ \mathbf{v}_k \right\}_{k \in \mathbb{N}}$이 힐베르트 공간 $H$에서 정의된 시퀀스라 하자. 유계 선형 작용소 $T : l^{2} \to H$ 가 다음과 같이 정의되어있다고 하자.
$$ T \left\{ c_{k} \right\}_{k \in \mathbb{N}} := \sum_{k=1}^{\infty} c_{k} \mathbf{v}_{k} $$
그러면 $T$의 수반 작용소 $T^{ \ast } : H \to l^{2}$는 다음과 같이 나타난다.
$$ T^{ \ast } \mathbf{v} = \left\{ \left\langle \mathbf{v} , \mathbf{v}_{k} \right\rangle_{H} \right\}_{k \in \mathbb{N}} $$
그 뿐만 아니라, 모든 $\mathbf{v} \in H$에 대해
$$ \sum_{k=1}^{\infty} \left| \left\langle \mathbf{v} , \mathbf{v}_{k} \right\rangle_{H} \right|^{2} \le \left\| T \right\|^{2} \left\| \mathbf{v} \right\|_{H}^{2} $$
$T$ 는 $\left\| T \right\| \le \sqrt{B}$를 만족하게끔 정의되었으므로
$$ \sum_{k=1}^{\infty} \left| \left\langle \mathbf{v} , \mathbf{v}_{k} \right\rangle \right|^{2} \le \left\| T \right\|^{2} \left\| \mathbf{v} \right\|^{2} \le B \left\| \mathbf{v} \right\|^{2} $$
따라서 $\left\{ \mathbf{v}_k \right\}_{k \in \mathbb{N}}$는 베셀 바운드 $B$를 가지는 베셀 시퀀스가 된다.
■
Ole Christensen, Functions, Spaces, and Expansions: Mathematical Tools in Physics and Engineering (2010), p75-76 ↩︎
 저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!
저희들의 저서 「줄리아 프로그래밍」이 2024 세종도서 학술부문에 선정되었습니다!

