logo

有限次元ノルム空間の完備性の証明 📂バナッハ空間

有限次元ノルム空間の完備性の証明

定理 1

有限次元のノルム空間は完備性を持つ。

説明

それにより、有限次元のベクトル空間はノルムが定義されるだけでバナッハ空間になる。特に、Rn\mathbb{R}^{n}やCn\mathbb{C}^{n}がよく使われるため、特に便利な事実だ。

証明

戦略：有限次元のベクトル空間であるという点を利用して、全てのベクトルを基底単位に分けた後、扱いやすいノルムを定義する。ノルムの同値関係を利用し、抽象的な計算を直接的な計算に変換する。

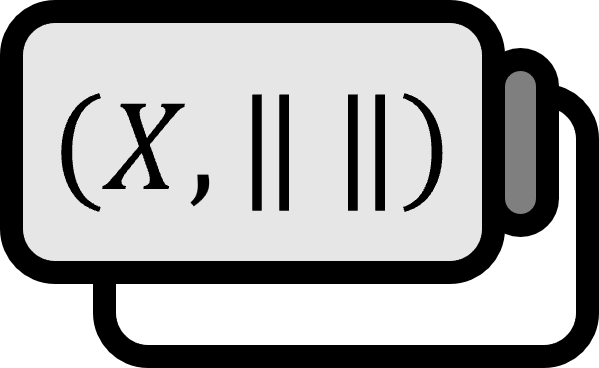
有限次元のノルム空間 (X,∥⋅∥0)(X, \| \cdot \|_{0} ) には、基底 {e1,⋯ ,en}\left\{ e_{1} , \cdots , e_{n} \right\} が存在する。

  • パート 1

    XXのコーシー数列{xk}k∈N\left\{ x_{k} \right\}_{k \in \mathbb{N} }を以下のように定義しよう。

    x1=λ1(1)e1+⋯+λn(1)en x_{1} = \lambda_{1}^{(1)} e_{1} + \cdots + \lambda_{n}^{(1)} e_{n}

    x2=λ1(2)e1+⋯+λn(2)en x_{2} = \lambda_{1}^{(2)} e_{1} + \cdots + \lambda_{n}^{(2)} e_{n}

    ⋮ \vdots

    xk=λ1(k)e1+⋯+λn(k)en x_{k} = \lambda_{1}^{(k)} e_{1} + \cdots + \lambda_{n}^{(k)} e_{n}

  • パート 2

    ∥λ1e1+⋯+λnen∥:=∑k=1n∣λk∣ \| \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n} \| : = \sum_{k=1}^{n} | \lambda_{k} |

    ノルム∥⋅∥\| \cdot \|を、線形結合の係数の絶対値をすべて足した値として定義してみよう。

XX は 有限次元のノルム空間なので ∥⋅∥0∼∥⋅∥\| \cdot \|_{0} \sim \| \cdot \| であり、あるm,M>0m , M > 0に対して

m∥xk−xm∥≤∥xk−xm∥0≤M∥xk−xm∥ m \| x_{k} - x_{m} \| \le \| x_{k} - x_{m} \|_{0} \le M \| x_{k} - x_{m} \|

  • パート 3

    ∥⋅∥\| \cdot \|の定義により

    m∥xk−xm∥≤∥xk−xm∥0 m \| x_{k} - x_{m} \| \le \| x_{k} - x_{m} \|_{0}

      ⟹  m(∣λ1(k)−λ1(m)∣+⋯+∣λn(k)−λn(m)∣)≤∥xk−xm∥0 \implies m \left( \left| \lambda_{1}^{(k)} - \lambda_{1}^{(m)} \right| + \cdots + \left| \lambda_{n}^{(k)} - \lambda_{n}^{(m)} \right| \right) \le \| x_{k} - x_{m} \|_{0}

    {xk}k∈N\left\{ x_{k} \right\}_{k \in \mathbb{N} }はコーシー数列なので、k,m→∞k,m \to \inftyのとき∥xk−xm∥0→0\| x_{k} - x_{m} \|_{0} \to 0である。すると、全ての1≤i≤n1 \le i \le nに対して

    lim⁡k,m→∞m(∣λi(k)−λi(m)∣)→0 \lim_{k,m \to \infty } m \left( \left| \lambda_{i}^{(k)} - \lambda_{i}^{(m)} \right| \right) \to 0

    したがって、{λi(k)}k∈N\left\{ \lambda_{i}^{(k)} \right\}_{k \in \mathbb{N}}はコーシー数列であり、C\mathbb{C}は完備空間なので、何らかのλi∈C\lambda_{i} \in \mathbb{C}に収束する。

  • パート 4

    x:=λ1e1+⋯+λnenx := \lambda_{1} e_{1} + \cdots + \lambda_{n} e_{n}とすると

    ∥xk−x∥0≤M∥xk−x∥ \| x_{k} - x \|_{0} \le M \| x_{k} - x \|

      ⟹  ∥xk−x∥0≤M(∣λ1(k)−λ1∣+⋯+∣λn(k)−λn∣) \implies \| x_{k} - x \|_{0} \le M \left( \left| \lambda_{1}^{(k)} - \lambda_{1} \right| + \cdots + \left| \lambda_{n}^{(k)} - \lambda_{n} \right| \right)

      ⟹  0≤lim⁡k→∞∥xk−x∥0≤lim⁡k→∞M(∣λ1(k)−λ1∣+⋯+∣λn(k)−λn∣) \implies 0 \le \lim_{k \to \infty} \| x_{k} - x \|_{0} \le \lim_{k \to \infty} M \left( \left| \lambda_{1}^{(k)} - \lambda_{1} \right| + \cdots + \left| \lambda_{n}^{(k)} - \lambda_{n} \right| \right)

      ⟹  lim⁡k→∞∥xk−x∥0=0 \implies \lim_{k \to \infty} \| x_{k} - x \|_{0} = 0

    したがって、XXのコーシー数列{xk}k∈N\left\{ x_{k} \right\}_{k \in \mathbb{N} }はx∈Xx \in Xに収束する。

■

  1. Kreyszig. (1989). Introductory Functional Analysis with Applications: p73. ↩︎