📂統計的検定

マン-ホイットニーU検定

仮説検定 ¹

二つの連続確率変数 $X, Y$ が与えられており、合計で $\left( n_{1} + n_{2} \right)$ 個のランダムサンプルが $X_{1} , \cdots , X_{n_{1}} \overset{\text{iid}}{\sim} X$ と $Y_{1} , \cdots , Y_{n_{2}} \overset{\text{iid}}{\sim} Y$ のように二種類の分布からサンプリングされたとする。便宜上 $X$ を第一の母集団、$Y$ を第二の母集団とする。

$X$ と $Y$ の累積分布関数をそれぞれ $F_{X}$, $F_{Y}$ とし，これらがロケーションファミリーに属すると仮定する。つまり，ある $\delta$ に対して $F_{X} (z) = F_{Y} (z + \delta)$ のように表されるとき，$\delta$ に関する次の仮説検定をマン＝ホイットニー $U$ 検定^{Mann-Whitney $U$ test}という。

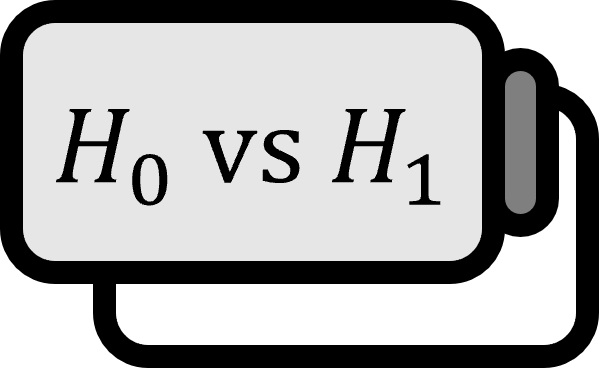
• $H_{0} : \delta = 0$：二つの母集団の分布は等しい。
• $H_{1} : \delta \ne 0$：二つの母集団の分布は等しくない。

検定統計量

これについて次のような検定統計量を定義する。

1. 全てのサンプルの中で $\left\{ X_{i} \right\}_{i=1}^{n_{1}}$ らの順位を足した値を $T_{1}$、全てのサンプルの中で $\left\{ Y_{j} \right\}_{j=1}^{n_{2}}$ らの順位を足した値を $T_{2}$ とする。$T_{1}$ と $T_{2}$ をウィルコクソン統計量^{Wilcoxon statistic}という。
2. $U_{1}$ は $X_{i}$ が $Y_{j}$ より大きい場合の個数、$U_{2}$ は $Y_{j}$ が $X_{i}$ より大きい場合の個数とする。$U_{1}$ と $U_{2}$ をマン＝ホイットニー統計量^{Mann-Whitney statistic}という。ただし、確率変数の値が正確に等しくて $X_{i} = Y_{j}$ となる場合はその確率が $P \left( X_{i} = Y_{j} \right) = 0$ であるためほとんどありえないものとして除外する。

検定統計量 $U_{1}$ は有意水準 $\alpha$ に対して次を満たす最大の整数 $u$ と比較して $U_{1} \le u$ であれば $H_{0}$ を棄却する。 $$ P \left( U_{1} \le u \right) \le \alpha / 2 $$ ここに出てきた棄却域の下限 $u$ については $U_{1}$ とともに別途説明する。

定理

• [1] $U$ の和と $T$ の和：二つのマン＝ホイットニー統計量 $U_{1}$, $U_{2}$ の和は次の通りである。 $$ U_{1} + U_{2} = n_{1} n_{2} $$ 二つのウィルコクソン統計量 $T_{1}$, $T_{2}$ の和は次の通りである。 $$ T_{1} + T_{2} = {{\left( n_{1} + n_{2} \right) \left( n_{1} + n_{2} + 1 \right)} \over 2} $$
• [2] $U$ と $T$ の関係：第一の母集団に対する $U_{1}$ と $T_{1}$ の関係は次の通りである。 $$ U_{1} = T_{1} - {{n_{1} \left( n_{1} + 1 \right)} \over 2} $$ 第二の母集団に対する $U_{2}$ と $T_{2}$ の関係は次の通りである。 $$ U_{2} = T_{2} - {{n_{2} \left( n_{2} + 1 \right)} \over 2} $$

説明

マン＝ホイットニー $U$ 検定^{Mann-Whitney $U$ test}はウィルコクソン順位和検定^{Wilcoxon rank-sum test}とも広く知られているノンパラメトリックな検定であり、二つの母集団が与えられていてその分布の形自体は不明でも、分布が同じか異なるかを調べたいときに用いる。

ただし、仮説検定の前提で述べたようにこの「異なる」というのは関数形そのものではなく位置（location）、例えば正規分布であれば母平均の差にのみ着目し母分散を含む他の要素までは扱わない点に注意する。

一方、定理[2]からわかるように、実際には $U$ と $T$ は単に定数を含むだけで統計量としてはほとんど同じである。それにもかかわらず両者が二つの名前を持つのはそれぞれ固有の理由があるためである。

ウィルコクソン順位和統計量

現実には、$U_{1}$ は $T_{1}$ を通じて計算されることが多い。単純に考えて $X_{i} > Y_{j}$ の場合を全てカウントするというのはこれらの比較のために $n_{1}$ 個のデータセットと $n_{2}$ 個のデータセットを一度は走査する必要があるため $O \left( n_{1} n_{2} \right)$ 程度の時間計算量を持つ。もしサンプル数が少なく時間的負担が小さいとしても単に和を計算するよりは複雑であり、理論を離れて実際に $X_{i} = Y_{j}$ のような例外的な同率（タイ） が発生する場合でも $T_{1}$ は一貫した結果を保証する。

マン＝ホイットニー $U$ 統計量

しかし実際に $U_{1}$ が計算される過程とは別に、検定そのものは $U_{1}$ の定義を根拠としている。もし帰無仮説が真であるという仮定の下でサンプルが抽出されたなら、最終的に $U_{1}$ の分布は確率の最も原初的な概念である頻度に依存するほかないためである。

検定統計量を紹介するとき棄却域の下限 $u$ は $P \left( U_{1} \le u \right) \le \alpha / 2$ を満たす最大の整数であるとしたが、実際には右辺はある関数 $h$ に対して次のように計算される。 $$ P \left( U_{1} \le u \right) \le \alpha / 2 \approx {\frac{ h \left( n_{1} , n_{2} , u \right) n_{1}! n_{2}! }{ \left( n_{1} + n_{2} \right)! }} $$ ここで $h \left( n_{1} , n_{2} , u \right)$ は帰無仮説 $H_{0}$ が真であるという仮定の下で $\left( n_{1} + n_{2} \right)$ 個のサンプル中に $U_{1} < u$ が起こる頻度を表す再帰関数であり、マンとホイットニーによって次が証明された²。 $$ \begin{align*} h \left( n_{1} , n_{2} , u \right) =& h \left( n_{1} - 1 , n_{2} , u - n_{2} \right) + h \left( n_{1} , n_{2} - 1 , u \right) \\ h \left( n_{1} , n_{2} , u \right) =& h \left( n_{2} , n_{1} , u \right) \\ h \left( n_{1} , n_{2} , 0 \right) =& h \left( n_{1} , 0 , u \right) = 1 \\ h \left( n_{1} , n_{2} , - \Delta \right) =& 0 \qquad , \Delta > 0 \end{align*} $$ これによれば $n_{1}$ と $n_{2}$ が与えられ、有意水準 $\alpha$ が変わるたびに $u$ の値も変化するため、次のような表を作って仮説検定に用いる。

多くの教科書はこのような表がなぜ現れるのか、また $U_{1}$ と $T_{1}$ の関係がどのように成立するかを省略しているが、証明過程を丁寧に見ると教科書の枠を超えた内容も簡単に納得できる。

証明

$I (X > Y)$ は $X > Y$ の場合にのみ1、そうでなければ0を取る指示関数とする。$R(Z)$ は全体サンプルにおける $Z$ の順位で、$R_{1} \left( X_{i} \right)$ は第一のサンプルにおける $X_{i}$ の順位、$R_{2} \left( Y_{j} \right)$ は第二のサンプルにおける $Y_{j}$ の順位とする。

[1]

$$ \begin{align*} U_{1} =& \sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}} I \left( X_{i} > Y_{j} \right) \\ U_{2} =& \sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}} I \left( X_{i} < Y_{j} \right) \end{align*} $$ $U_{1}$ と $U_{2}$ は全ての $i = 1, \cdots , n_{1}$ と $j = 1, \cdots , n_{2}$ に対して $X_{i}$ と $Y_{j}$ を比較して上のように表せ、これらの和は次の通りである。 $$ U_{1} + U_{2} = \sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}} I \left( X_{i} \ne Y_{j} \right) = n_{1} n_{2} $$

等差数列の和の公式: 初項が $a$ で公差が $d$ の等差数列 $a_{n} = a+(n-1)d$ について $$ \sum_{k=1}^{n} a_{k}= {{n \left\{ 2a + (n-1)d \right\} } \over {2}} $$

サンプルサイズが $\left( n_{1} + n_{2} \right)$ であるから順位の総和は次の通りである。 $$ T_{1} + T_{2} = {{\left( n_{1} + n_{2} \right) \left( n_{1} + n_{2} + 1 \right)} \over 2} $$

■

[2]

全体サンプルでの $X_{i}$ の順位 $R \left( X_{i} \right)$ というのは第一の母集団での順位 $R_{1} \left( X_{i} \right)$ に加えて $X_{i}$ より小さい $Y_{j}$ の合計でなければならず、これを式で表すと次の通りである。 $$ R \left( X_{i} \right) = R_{1} \left( X_{i} \right) + \sum_{j=1}^{n_{2}} I \left( X_{i} > Y_{j} \right) $$ ウィルコクソン順位和統計量は $T_{1} = \sum_{i=1}^{n_{1}} R \left( X_{i} \right)$ であるから、全ての $i = 1, \cdots , n_{1}$ について $R \left( X_{i} \right)$ を足すと次の通りである。 $$ \begin{align*} \sum_{i=1}^{n_{1}} R \left( X_{i} \right) =& \sum_{i=1}^{n_{1}} R_{1} \left( X_{i} \right) + \sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}} I \left( X_{i} > Y_{j} \right) \\ \sum_{i=1}^{n_{1}} R \left( X_{i} \right) =& T_{1} \\ \sum_{i=1}^{n_{1}} R_{1} \left( X_{i} \right) =& \sum_{i=1}^{n_{1}} i = {{n_{1} \left( n_{1} + 1 \right)} \over 2} \\ \sum_{i=1}^{n_{1}} \sum_{j=1}^{n_{2}} I \left( X_{i} > Y_{j} \right) =& U_{1} \end{align*} $$ これを改めて書くと次の通りである。 $$ U_{1} = T_{1} - {{n_{1} \left( n_{1} + 1 \right)} \over 2} $$ 同様の方法で $U_{2}$ と $T_{2}$ の関係も証明できる。

■