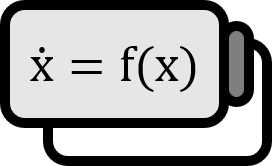📂動力学

自律システムのオメガリミットセット

定義

距離空間 $X$ と関数 $f : X \to X$ について、次のようなベクトル場が微分方程式として与えられているとする。 $$ \dot{x} = f(x) $$ このシステムのフロー $\phi ( t, x )$ とある点 $x_{0} \in X$ に対して、$t_{i} \to \infty$ のとき $$ \phi \left( t_{i} , x_{0} \right) \to x $$ を満たす時間のシーケンス $\left\{ t_{i} \right\} \subset \mathbb{R}$ が存在すれば、$ x \in X$ を $x_{0}$ の オメガリミットポイント と呼ぶ。$x_{0}$ のオメガリミットポイントの集合を $x_{0}$ のオメガリミットセットと呼び、$\omega \left( x_{0} \right)$ と表現する。

説明

上記の定義で他のものはそのままにして $t_{i} \to - \infty$ に置き換えると アルファリミットポイント 、アルファリミットセット 、$\alpha \left( x_{0} \right)$ と変わる。アルファとオメガはギリシャアルファベットの最初と最後であり、時間が負の無限大（最初）に行くときは $\alpha \left( x_{0} \right)$ を扱い、正の無限大（最後）に行くときは $\omega \left( x_{0} \right)$ を扱うので、直感的なセンスとしては理解できる命名と言えるだろう。リミットポイントは集積点として翻訳され、位相数学とは異なり、フローが与えられているため、時間が過去に流れるか未来に流れるかに注意する必要がある。もちろん、ほとんどの場合、興味を引くのは未来、つまりオメガリミットだろう。

少なくとも扱うシステムが常微分方程式として与えられている以上、$x_{0}$ を初期位置とするオメガリミットセットはカーブの形状または一点である可能性が高い。点が動きながら作る軌跡が面積を持つ領域を成すことはないとは言えないが、ベクトル場の定義によれば、そのようなことは実質不可能と見なされる。

性質

オメガリミットセットの性質: ¹全体空間がユークリッド空間 $X = \mathbb{R}^{n}$ であり、フロー $\phi_{t} ( \cdot )$ においてコンパクト 陽不変集合 $\mathcal{M}$ のある点 $p \in \mathcal{M}$ が与えられているとする。

• [1]: $\omega (p) \ne \emptyset$
• [2]: $\omega (p)$ は閉集合である。
• [3]: $\omega (p)$ はフローに不変である。つまり、$\omega (p)$ は軌道の合集合である。
• [4]: $\omega (p)$ は連結空間である。

もちろん、これらの性質はアルファリミットについても同様である。

性質 [1]の証明

$p \in \mathcal{M}$ と $\displaystyle \lim_{k \to \infty} t_{k} = \infty$ である時間のシーケンス $\left\{ t_{k} \right\} \subset \mathbb{R}$ に対して次のような集合 $\Phi (p) \subset \mathcal{M}$ を定義する。 $$ \Phi (p) := \left\{ p_{k} : p_{k} = \phi_{t_{k}} (p) \right\} $$ $\mathcal{M}$ はコンパクトなので、ボルツァーノ・バイアストラースの定理に従って $\omega (p)$ への一点に収束する $\Phi (p)$ のサブシーケンスが存在し、したがって $\omega (p) \ne \emptyset$

■

性質 [2]の証明

$\omega (p)^{c}$ がオープンセットであることを示せば十分である。$\omega (p)$ の外の任意の一点 $q \notin \omega (p)$ を取ると、ある $T > 0$ に対して $$ \left\{ \phi_{t} (p) : t \ge T \right\} \cap \mathcal{N} (q) = \emptyset $$ を満たす $q$ の近傍 $\mathcal{N} (q)$ が存在しなければならない。言い換えれば、$q$ は $\omega (p)$ と非交差するオープンセットに含まれなければならないが、この $q$ は $\omega (p)$ の外の任意の点であるため、$\omega (p)^{c}$ はオープンセットでなければならない。

■

性質 [3]の証明

まず、すべての $q \in \omega (p)$ と $s \in \mathbb{R}$ について $\phi_{s} ( q )$ が存在すると仮定する。この仮定は元々証明が必要で可能であるが、内容に対してあまり意味がないため省略する。 $$ q \in \omega (p) \\ \widetilde{q} := \phi_{s} (q) $$ とし、$\lim_{k \to \infty } t_{k} = \infty$ のとき $\phi_{t_{k}} (p) \to q$ になるようにする時間のシーケンス $\left\{ t_{k} \right\} \subset \mathbb{R}$ を取る。そうすると、$k \to \infty$ のとき $$ \phi_{t_{k} + s} (p) = \phi_{s} \left( \phi_{t_{k} } (p) \right) \to \widetilde{q} $$ となるので $\widetilde{q} \in \omega (p)$ であり、よって $\omega (p)$ は不変である。

■

性質 [4]の証明

$\omega (p)$ が連結空間でないと仮定すると、次を満たすオープンセット $V_{1} , V_{2} \subset \mathbb{R}^{n}$ が存在する。 $$ \omega (p) \subset V_{1} \cap V_{2} \\ \omega (p) \cap V_{1} \ne \emptyset \\ \omega (p) \cap V_{2} \ne \emptyset \\ V_{1} \cap V_{2} = \emptyset $$ これについて $K := \mathcal{M} \setminus \left( V_{1} \cup V_{2} \right)$ とする。$V_{1}, V_{2}$ の定義によれば、$p \in \mathcal{M}$ の軌道は $V_{1}, V_{2}$ の両側にまたがり、すべての $T > 0$ について $\phi_{t} (p) \in K$ を満たす $t > T$ が存在するので、$k \to \infty$ のとき $t_{k} \to \infty$ かつ $\phi_{t_{k}} (p) \in K$ である時間のシーケンス $\left\{ t_{k} \right\}$ を取ることができる。なぜなら、$V_{1}$ と $V_{2}$ が離れていて両方の集合が $\omega (p)$ と互いに素でないので $\phi_{t}$ が $V_{1}$ と $V_{2}$ のどちらかに永遠に留まることはできず、反対側に渡って $K$ を通過せざるを得ないからだ。$V_{1} , V_{2}$ はオープンセットなので $K$ はコンパクトであり、ボルツァーノ・バイアストラースの定理に従って $\phi_{t_{k}} (p)$ が $q \in K$ に収束するようにする $\left\{ t_{k} \right\}$ のサブシーケンスが存在するが、これはつまり $q \notin V_{1} \cup V_{2}$ である。しかし、オメガリミットセットの定義から $q \in \omega (p)$ でなければならないので $\omega (p) \subset V_{1} \cap V_{2}$ と矛盾する。したがって、$\omega (p)$ は連結空間である。

■