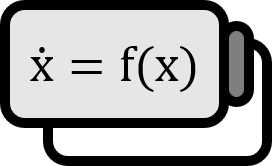📂動力学

力学におけるリュービルの定理の証明

定理

ユークリッド空間 $\mathbb{R}^{n}$ と関数 $f : \mathbb{R}^{n} \to \mathbb{R}^{n}$ について次のようなベクトル場が微分方程式で与えられているとする。 $$\dot{x} = f(x)$$ このシステムのフロー $\phi_t ( \cdot )$ と領域 $D_{0} \subset \mathbb{R}^{n}$ について $D_{t} := \phi_{t} \left( D_{0} \right)$ をフローに従って時間 $t$ が経過して移動した領域、そのボリュームを $V(t) \equiv V \left( D_{t} \right)$ として示す。もし $\nabla \cdot f = 0$ ならすべての $D_{0} \subset \mathbb{R}^{n}$ と $t \in \mathbb{R}$ について次が成り立つ。 $$V \left( D_{t} \right) = V \left( D_{0} \right)$$

数式の説明

$\nabla \cdot f$ はベクトル場の発散で、ベクトル場が広がったり集まったりする様子を示す。

$V$ はベクトル場で与えられた領域のボリュームを意味する。リウヴィルの定理は言葉より数式の方が簡単だが、簡単に言えば、発散がどこでも $0$ ならばフローが移動した領域のボリュームが変わらないということである。

証明 ¹

戦略: ベクトル微積分学を少し使えばよい。次のようにベクトル関数と各ベクトルの軸を表せば、解析学と線形代数の基本的なツールによる計算だけで直接演繹される。 $$f := \left( f_{1} , \cdots , f_{n} \right) \\ x := \left( x_{1} , \cdots , x_{n} \right)$$

---

Part 1. $t_{0} = 0$ のとき $\displaystyle \left.{{ d V } \over { d t }}\right|_{t = t_{0}} = \int_{D_{0}} \nabla \cdot f dx$

ボリュームの定義: $\textbf{u} \in \mathbb{R}^{n}$ がベクトル関数 $\textbf{f} : \mathbb{R}^{n} \to \mathbb{R}^{n}$ によって $\textbf{f} \left( \textbf{u} \right) = \left( f_{1} (\textbf{u}) , \cdots , f_{n} (\textbf{u}) \right)$ として変換されるとき、$D$ のボリュームは次のようになる。 $$V(D) = \int_{D} \left| {{ \partial \textbf{f} (\textbf{u}) } \over { \partial \textbf{u} }} \right| d u_{1} d u_{2} \cdots d u_{n}$$

ボリュームの定義に従って $$V(t) = \int_{D_{0}} \det {{ \partial \phi_{t} (x) } \over { \partial x }} dx$$ フロー $\phi_{t} (x)$ を $t=0$ でテイラー展開すると $$\phi_{t} (x) = x + f(x) t + O \left( t^{2} \right)$$ $x$ で偏微分すると $n\times n$ 単位行列 $E$ に対して $${{ \partial \phi_{t} (x) } \over { \partial x }} = E + {{ \partial f } \over { \partial x }} t + O \left( t^{2} \right)$$ のように示すことができる。すると、その行列式は $$\begin{align*} \det {{ \partial \phi_{t} (x) } \over { \partial x }} =& \det \left[ E + {{ \partial f } \over { \partial x }} t \right] + O \left( t^{2} \right) \\ =& 1 + \text{tr} \left[ {{ \partial f } \over { \partial x }} \right] t + O \left( t^{2} \right) \\ =& 1 + \left( {{ d f_{1} } \over { d x_{1} }} + \cdots + {{ d f_{n} } \over { d x_{n} }} \right) t + O \left( t^{2} \right) \\ =& 1 + t \nabla \cdot f + \mathcal{O} \left( t^{2} \right) \end{align*}$$ ここで $\text{tr}$ はトレースTraceで、行列の対角成分の合計を意味する。両辺に $\int_{D_{0}} \cdot dx$ を取ると $$\begin{align*} V(t) =& \int_{D_{0}} \det {{ \partial \phi_{t} (x) } \over { \partial x }} dx \\ =& \int_{D_{0}} 1 dx + \int_{D_{0}} t \nabla \cdot f dx + O \left( t^{2} \right) \\ =& V \left( D_{0} \right) + t \int_{D_{0}} \nabla \cdot f dx + O \left( t^{2} \right) \end{align*}$$ $V \left( D_{0} \right) = V(0)$ を左辺に移すと $$V(t) - V(0) = t \int_{D_{0}} \nabla \cdot f dx + O \left( t^{2} \right)$$ 両辺を $(t - 0)$ で割ると $${{ V(t) - V(0) } \over { t-0 }} = \int_{D_{0}} \nabla \cdot f dx + O \left( t^{1} \right)$$ テイラー近似を $t = 0$ 近傍で用いたので、$t \to 0$ のとき $O \left( t^{1} \right) \to 0$ であるから、 $$\left.{{ d V } \over { d t }}\right|_{t = 0} = \int_{D_{0}} \nabla \cdot f dx$$

---

Part 2. $t = t_{0}$ への拡張

$y := \phi_{t_{0}} (x)$ と仮定すると、Part 1.の議論を同じように進めて次を得る。 $$\left.{{ d V } \over { d t }}\right|_{t = t_{0}} = \int_{D_{0}} \nabla \cdot f dy$$ ある定数 $c \in \mathbb{R}$ に対して $\nabla \cdot f = c$ なら、 $$\left.{{ d V } \over { d t }}\right|_{t = t_{0}} = \int_{D_{0}} \nabla \cdot f dy = \int_{D_{0}} c dy = c \int_{D_{0}} dy$$ $y$ は $x$ を時間 $t_{0}$ だけフローに従って変換されたものであるから、$\int_{D_{0}} dy$ は $t_{0}$ 時点のボリュームとなる。これは任意の $t_{0} \in \mathbb{R}$ に対しても同様であるから、 $$V’ = c V$$ 上記の微分方程式は自明な解 $V(t) = e^{ct} V (0)$ を持つ。

---

Part 3.

上記 Part 2. の最後の式で $c = 0$ なら $V(t) = e^{ct} V (0) = V(0)$ である。

■

参考文献

• 複素解析におけるリウヴィルの定理