📂バナッハ空間

ハーン-バナッハの拡張定理

定理¹

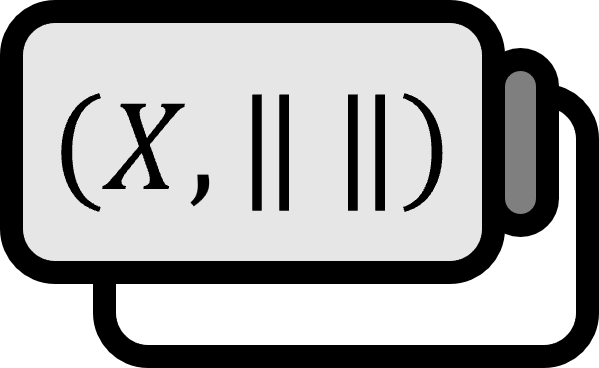
$(X, \left\| \cdot \right\|)$をノルム空間としよう。$Y \subset X$とする。そして、$Y$の線形汎関数$y^{\ast} \in Y^{\ast}$が与えられたとする。すると、以下の式を満たす$X$の線形汎関数$x^{\ast} \in X^{\ast}$が存在する。

$$\begin{equation} x^{\ast}(y)=y^{\ast}(y),\quad \forall y \in Y \end{equation}$$

$$\begin{equation} \| x^{\ast}\|_{X^{\ast}} = \| y^{\ast}\|_{Y^{\ast}} \end{equation}$$

説明

簡単に言うと、部分空間の双対を全空間の双対に拡張できるということだ。つまり、部分空間のすべての線形汎関数には、同じ関数値、ノルムを持つ全空間の線形汎関数が対になるものがある。また、ノルム空間$X$を$\mathbb{ C}$-ベクトル空間として扱おう。

補助定理：セミノルムに関するハーン-バナッハ定理

$X$は$\mathbb{C}$-ベクトル空間であって、$Y \subset X$とする。$p : X \to \mathbb{ R}$を$X$のセミノルムとしよう。そして、以下の条件を満たす$Y$の線形汎関数と仮定しよう。

$$| y^{\ast}(y) | \le p(y),\quad \forall y\in Y$$

すると、以下の条件を満たす$X$の線形汎関数$x^{\ast} : X \to \mathbb{C}$が存在する。

$$x^{\ast}(y)=y^{\ast}(y),\quad \forall y \in Y$$

$$| x^{\ast}(x) | \le p(x),\quad \forall x \in X$$

証明

$X$と$Y$のノルムを$\left\| \cdot \right\|$、$X^{\ast}$と$Y^{\ast}$のノルムを$\left\| \cdot \right\|_{X^{\ast}}$、$\left\| \cdot \right\|_{Y^{\ast}}$として表そう。$p : X \to \mathbb{R}$が以下のように定義された関数だとしよう。

$$p(x)=\|y^{\ast}\|_{Y^{\ast}} \|x \|_{X},\quad x\in X$$

すると$p$は準線形であることが示される。定義により$0 \le p$なので$p$はセミノルムである。また、以下の式が成り立つ。

$$\begin{align*} y^{\ast}(y) \le & | y^{\ast}(y) | \\ =&\ \left| \|y\| \frac{1}{\| y\|} y^{\ast}(y) \right| \\ =&\ \|y\| \left| y^{\ast}\left( \frac{y}{\|y\|} \right) \right| \\ \le & \|y\| \left\|y^{\ast}\right\|_{Y^{\ast}} \\ =&\ p(y) \end{align*}$$

三行目で$\|y\|$は定数なので絶対値の外に出ることができ、$y^{\ast}$が線形なので$\frac{1}{\|y\|}$が関数の中に入った。また、四行目は$\left\| \frac{y}{\|y\|} \right\| =1$であり双対のノルムの定義により$\| y^{\ast}\|_{Y^{\ast}}=\sup \limits_{\substack{ \|y\| \le 1 \\ y\in Y}} |y^{\ast}(y)|$なので成り立つ。したがって、補助定理を使う条件が満たされたので、以下の条件を満たす$X$の線形汎関数$x^{\ast} : X \to \mathbb{ C}$が存在する。

$$x^{\ast}(y)=y^{\ast}(y), \quad \forall y \in Y$$

$$\begin{equation} | x^{\ast}(x) | \le p(x),\quad \forall x \in X \end{equation}$$

最初の条件は$(1)$と同値である。$(3)$により、

$$|x^{\ast}(x)| \le p(x) =\|y^{\ast}\|_{Y^{\ast}} \|x\|$$

双対のノルムの定義により、

$$\|x^{\ast}\|_{X^{\ast}} = \sup \limits_{\substack{ \|x\| \le 1 \\ x\in X}}\|y^{\ast}\|_{Y^{\ast}} \|x\| = \|y^{\ast}\|_{Y^{\ast}}$$

したがって、$(2)$の条件を満たす。

■

結論

1

$X$がノルム空間で、$x_{0} \in X$であるとする。すると、以下の条件を満たす$x^{\ast} \in X^{\ast}$が存在する。

$$\|x^{\ast}\|_{X^{\ast}} = 1,\quad x^{\ast}(x_{0}) = \| x_{0}\|$$

証明

$Y=\left\{ \lambda | \lambda x_{0} \in \mathbb{ R}\right\}$としよう。すると、$Y$は$X$の部分空間になる。今、$Y$の線形汎関数$y^{\ast} : Y \to \mathbb{R}$を以下のように定義しよう。

$$y^{\ast}(y)=y^{\ast} (\lambda x_{0}):=\lambda \|x_{0}\|,\quad y=\lambda x_{0}\in Y$$

$y^{\ast}$が実際に線形になることは簡単に確認できるので省略する。$y^{\ast}$の定義により、

$$| y^{\ast}(y) |=\lambda\|x_{0} \|=\|\lambda x_{0}\|=\| y\|$$

双対のノルムの定義により$\| y^{\ast}\|_{Y^{\ast}}=\sup \limits_{\substack{ \|y\| \le 1 \\ y\in Y}} |y^{\ast}(y)|$なので、

$$\begin{equation} \|y^{\ast}\|_{Y^{\ast}} = 1 \end{equation}$$ また、

$$y^{\ast}(x_{0})=\|x_{0}\| \tag{5}$$

ハーン-バナッハ拡張定理により、与えられた$y^{\ast}$に対して$\|x^{\ast}\|_{X^{\ast}} = 1 = \|y^{\ast}\|_{Y^{\ast}}$であり、$x^{\ast}(y)=y^{\ast}(y),\forall y \in Y$を満たす$X$の線形汎関数$x^{\ast}$が存在する。この時$(4)$、$(5)$により、

$$\|x^{\ast}\|_{X^{\ast}} = \|y^{\ast}\|_{Y^{\ast}} = 1$$

$$x^{\ast}(x_{0})=y^{\ast}(x_{0})=\| x_{0}\|$$

■

2

$X$は$\mathbb{C}$-ベクトル空間であり、$Y \subset S$が共に$X$の部分空間であるとする。もし$s \in S$が$d (s, Y) = \delta > 0$であれば、以下を満たす$x^{\ast} \in X^{\ast}$が存在する。

$$\left\| x^{\ast} \right\|_{X^{\ast}} \le 1$$

$$\begin{align*} y^{\ast} (s) =&\ y^{\ast} (s) = \delta, \quad s \in (S \setminus Y) \\ x^{\ast} (y) =&\ y^{\ast} (y) = 0, \quad y \in Y \end{align*}$$

---

$d \left( s, Y \right)$は点$s$と集合$Y$との最も近い距離、つまり$d (s,Y) := \inf \limits_{y \in Y} \left\| s-y \right\|$を表す。

証明²

$$S := Y + \mathbb{C} s = \left\{ y + \lambda s : y \in Y , \lambda \in \mathbb{C} \right\}$$

とすると、$S \subset X$である。関数$y^{\ast} : S \to \mathbb{C}$を

$$y^{\ast} \left( y + \lambda s \right) := \lambda \delta$$

のように定義すると、$y^{\ast}$は当然線形性を持つ。今、$y^{\ast}$が関数であるか確認しよう。$y_{1} + \lambda_{1} s = y_{2} + \lambda_{2} s$とし、$\lambda_{1} \ne \lambda_{2}$と仮定すると、$y_{1} - y_{2} = \left( \lambda_{2} - \lambda_{2} \right) s$なので$\displaystyle s = {{ 1 } \over { \lambda_{2} - \lambda_{1} }} \left( y_{1} - y_{2} \right)$であり、$Y$はベクトル空間なので加法に閉じていなければならないため、$s \in Y$でなければならない。しかし、これは$d (s, Y) > 0$と矛盾するので$\lambda_{1} = \lambda_{2}$でなければならない、

$$y^{\ast} \left( y_{1} + \lambda_{1} s \right) = \lambda_{1} \delta = \lambda_{2} \delta = y^{\ast} \left( y_{2} + \lambda_{1} s \right)$$

したがって、$y^{\ast}$は関数としてうまく定義される。すべての$y + \lambda s \in S$に対して、

$$\begin{align*} \left| y^{\ast} (y + \lambda s) \right| =&\ \left| \lambda \delta \right| \\ =&\ \left| \lambda \right| d (s,Y) \\ =&\ \left| \lambda \right| \inf_{y \in Y} \left\| s-y \right\| \\ =&\ \left\| s- \lambda y \right\| \\ \le& \left\| y + \lambda s \right\| \end{align*}$$ よって、$y^{\ast}$は有界で、特に$\left\| y^{\ast} \right\| \le 1$である。$y^{\ast} : S \to \mathbb{C}$が有界線形関数であり、ハーン-バナッハ定理により、すべての$s \in S$に対して、$x^{\ast}(s) = y^{\ast}(s)$を満たす$x^{\ast} \in X^{\ast}$が存在する。一方、$y^{\ast}$の定義から$\lambda = 0$を代入すると、$y^{\ast} (y + 0 s) = 0$なので、すべての$y \in Y$に対して、

$$y^{\ast} (y ) = x^{\ast}(y) = 0$$

また、$y^{\ast}$は線形なので、

$$y^{\ast} (s) = y^{\ast} (y) + 1 y^{\ast} (s)= y^{\ast} (y + 1s) = 1 \delta$$

つまり、$s \in (S \setminus Y)$に対して、

$$y^{\ast} (s) = x^{\ast}(s) = \delta$$

■

付録

付録1

$x_{1},x_{2} \in X$で、$\lambda \in \mathbb{C}$とする。すると、

$$\begin{align*} p(x_{1} + x_{2}) =&\ \|y^{\ast}\|_{Y^{\ast}} \|x_{1} + x_{2} \| \\ \le & \|y^{\ast}\|_{Y^{\ast}} \big(\| x_{1}\| +\|x_{2}\| \big) \\ =&\ \|y^{\ast}\|_{Y^{\ast}} \|x_{1}\| + \|y^{\ast}\|_{Y^{\ast}} \|x_{2}\| \\ =&\ p(x_{1})+p(x_{2}) \end{align*}$$

$$\begin{align*} p(\lambda x_{1}) =&\ \|y^{\ast}\|_{Y^{\ast}} \|\lambda x_{1} \| \\ =&\ |\lambda | \|y^{\ast}\|_{Y^{\ast}} \|x_{1}\| \\ =&\ | \lambda| p(x_{1}) \end{align*}$$

よって、$p$は準線形である。

■

付録2

$X$がベクトル空間であるので、$X$の要素に定数をかけたものはやはり$X$の要素である。したがって、$Y$は$X$の部分集合である。部分集合$Y$が部分空間になるためには、加法とスカラー倍に関して閉じていることを示す必要がある。$y_{1}=\lambda_{1}x_{0} \in Y$、$y_{2}=\lambda_2x_{0} \in Y$、$\lambda_{1}, \lambda_2, k \in \mathbb{R}$であり、$\lambda_{1}+\lambda_2=\lambda_{3}\in \mathbb{R}$、$k\lambda_{1}=\lambda_{4}\in \mathbb{ R}$とする。すると、

$$y_{1}+y_{2}=\lambda_{1} x_{0} + \lambda_2 x_{0}=\lambda_{3}x_{0}\in Y$$

$$ky_{1}=k(\lambda_{1}x_{0})=(k \lambda_{1})x_{0}=\lambda_{4} x_{0} \in Y$$

したがって、$Y$は$X$の部分空間である。

■