logo

極座標によって定義される直線 📂トモグラフィ

極座標によって定義される直線

説明

極座標で定められる直線

그림1.png

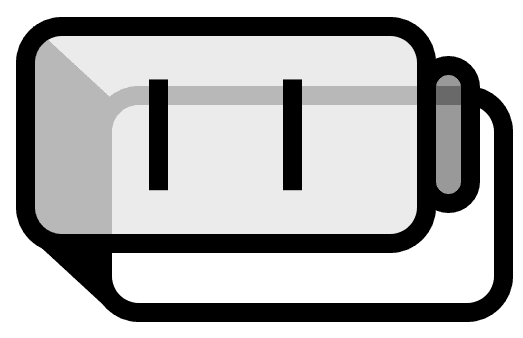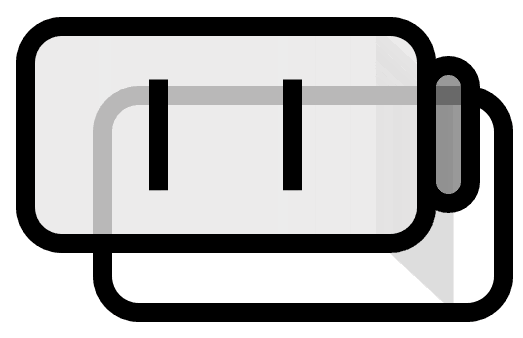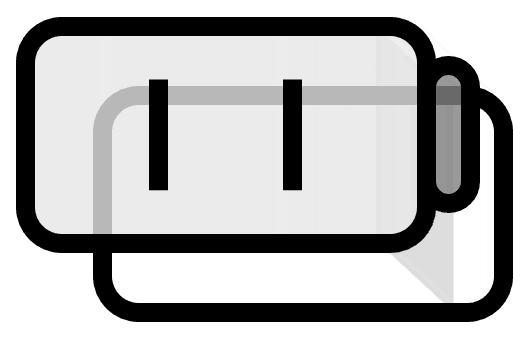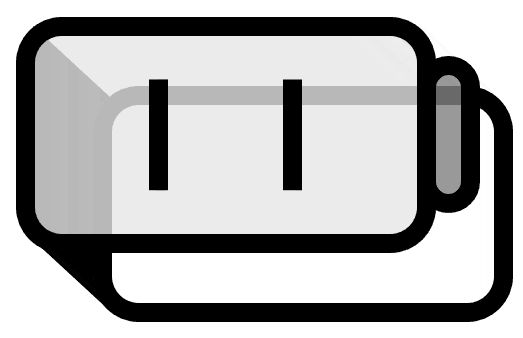
図(1)のような直線は、傾きaaとyy切片bbで定まる。傾きと切片だけあれば、平面上のすべての直線を表せるように思えるが、そうではない。正確には関数として直線のみを示すことができる。だから図(2)のように、xx軸に垂直な直線は、傾きと切片で表せない。

그림2.png

今、図(3)を見よう。この直線は原点からssだけ離れていて、単位ベクトルθ=(cos⁡θ,sin⁡θ)\boldsymbol{\theta} = (\cos \theta, \sin \theta)に垂直な直線だ。したがって、極座標(s,θ)(s, \theta)によって、平面上の直線がひとつ決まるとわかる。また、傾きと切片を使う方法と異なり、図(4)のようにxx軸に垂直な直線も極座標で表現できる。

このような直線の表記法は、ラドン変換などで線積分を表す際に有用だ。

直線上の点

그림3.png

上の図のように、パラメーターttを加えると、直線上の一点を表せる。θ=(cos⁡θ,sin⁡θ)\boldsymbol{\theta}=(\cos \theta, \sin \theta)、θ⊥=(−sin⁡θ,cos⁡θ)\boldsymbol{\theta}^\perp=(-\sin \theta, \cos \theta)とすると、

P= sθ+tθ⊥= (scos⁡θ,ssin⁡θ)+(−tsin⁡θ,tcos⁡θ)= (scos⁡θ−tsin⁡θ,ssin⁡θ+tcos⁡θ) \begin{align*} P =&\ s\boldsymbol{\theta} + t \boldsymbol{\theta}^\perp \\ =&\ (s\cos\theta, s\sin\theta) + (-t \sin\theta, t \cos\theta) \\ =&\ (s\cos\theta-t \sin\theta, s\sin\theta+ t \cos\theta) \end{align*}

するとssとθ\thetaで決まる直線ls,θl_{s, \theta}は、次の集合と同じだ。

ls,θ={sθ+tθ⊥:t∈R} l_{s, \theta} = \left\{ s\boldsymbol{\theta} + t \boldsymbol{\theta}^\perp : t \in \mathbb{R} \right\}

また−s(cos⁡(θ+π),sin⁡(θ+π))=s(cos⁡θ,sin⁡θ)-s \big(\cos(\theta + \pi), \sin (\theta + \pi)\big) = s(\cos \theta, \sin \theta)であるため、ssが負の場合は、次のように定義する。

l−s,θ+π:=ls,θ l_{-s, \theta+\pi} := l_{s, \theta}

一般化

Rn\mathbb{R}^{n}で、原点からssだけ離れていて、単位ベクトルθ∈Sn−1\boldsymbol{\theta} \in \mathbb{S}^{n-1}に垂直な直線は、次のようになる。

ls,θ={sθ+tθ⊥:t∈R} l_{s, \boldsymbol{\theta}} = \left\{ s\boldsymbol{\theta} + t \boldsymbol{\theta}^\perp : t \in \mathbb{R} \right\}