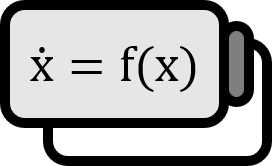📂動力学

ファン・デル・ポール振動子

ダフィング方程式¹

$$\ddot{x} + \delta \dot{x} + \alpha x + \beta x^{3} = \gamma \cos \left( \omega t \right)$$

変数

• $t$: 時間を表す。
• $x$: (例えば、粒子の)位置を$1$次元空間で表す。
• $\dot{x}$: (粒子の)速度を表す。
• $\ddot{x}$: (粒子の)加速度を表す。

パラメータ

• $\delta$：ダンピングを制御し、摩擦に似た役割を果たす。
• $\alpha$：剛性を制御し、ばね定数に似て潜在エネルギーに影響を与える。
• $\beta$：非線形復元力を制御し、$\beta = 0$の時、強制ダンプされた調和振動子を記述する。
• $\gamma$：駆動力の大きさを制御し、$\gamma = 0$の時、自立システムになりUnforced Duffing Oscillatorと呼ばれる。
• $\omega$：角周波数を制御する。

古典力学の意味

ダフィングオシレーターはゲオルク・ダフィングの名前がつけられた非自治系であり、運動エネルギーと潜在エネルギーを持つオブジェクトの振動を表す。$x$は、たとえば吊り下げられたばねの長さを表すことができ、様々なパラメータがあるため、それよりも複雑な状況を表すことができる。

ダフィング方程式は、古典力学の関心がある場合の物理的な意味での形である。動力学では、数学的な性質に関心がある場合、系は以下の連立常微分方程式の形で表すことを好む。

ダフィングオシレーターシステム²

$$\begin{align*} \dot{x} =& y \\ \dot{y} =& \gamma \cos ( \omega t ) - \alpha x - \beta x^{3} - \delta y \end{align*}$$

変数

• $x(t)$: (例えば、粒子の)位置を$1$次元空間で表す。
• $y(t)$: (粒子の)速度を表す。

パラメータ

• $\delta$：ダンピングを制御し、摩擦に似た役割を果たす。
• $\alpha$：剛性を制御し、ばね定数に似て潜在エネルギーに影響を与える。

$\beta$：非線形復元力を制御し、$\beta = 0$の時、強制ダンプされた調和振動子を記述する。

• $\gamma$：駆動力の大きさを制御し、$\gamma = 0$の時、自立システムになりUnforced Duffing Oscillatorと呼ばれる。
• $\omega$：角周波数を制御する。

動力学的分析

前述の通り、$\gamma = 0$であればダフィングオシレーターは自立システムになり、教科書的な例では、$\alpha = -1$、$\beta = 1$のようにUnforced Damped Duffing Oscillatorの形に簡略化して使われることが多い。 $$\begin{align*} \dot{x} =& y \\ \dot{y} =& x - x^{3} - \delta y \end{align*}$$ 動力学では、これらの微分方程式自体の解にそれほど関心がない。むしろ、簡単に解ける場合、その理由だけで動力学のツールを使って分析する価値を感じない場合がある。興味は、パラメータ$\delta$の変化によってシステム自体がどのように変化するかにある。機械的に、このシステムが意味を持つためには、ダンピングを表す$\delta$が負であってはならないため、 $$\begin{align*} \dot{x} =& y \\ \dot{y} =& x - x^{3} - \delta y \qquad , \delta \ge 0 \end{align*}$$ でなければならない。もちろん、このシステムの平衡点$(\dot{x} , \dot{y}) = (0,0)$は次のように与えられる。 $$(x,y) = (0,0) , (\pm 1 , 0)$$ このように、このシステムに対する動力学的な分析のためには、式を非線形関数$f,g$として表す必要がある。 $$\begin{align*} \dot{x} =& f(x,y) \\ \dot{y} =& g(x,y ; \delta) \qquad , \delta \ge 0 \end{align*}$$ これはベクトル表現で$\mathbf{x} ' = \mathbf{f} (\mathbf{x})$として表せ、記号に混乱がなければ、単に$\dot{x} = f(x)$とも書ける。もちろん、この場合は$x,y$が登場して非常に混乱するため、ある非線形関数$\mathbf{f} : \mathbb{R}^{2} \to \mathbb{R}^{2}$が$\mathbf{x} ' = \mathbf{f} (\mathbf{x})$として表されると明確に記述する必要がある。この表現を使用する際、システムのヤコビアンは次のように求められる。 $$D \mathbf{f} = \begin{bmatrix} 0 & 1 \\ 1 - 3 x^{2} & - \delta \end{bmatrix}$$ さて、３つの平衡点$(0,0) , (\pm 1 , 0)$に対してリアプノフ安定性を知りたければ、一つ一つ代入してみればいい。 $$D \mathbf{f} (0,0) = \begin{bmatrix} 0 & 1 \\ 1 & - \delta \end{bmatrix} \\ D \mathbf{f} (\pm1,0) = \begin{bmatrix} 0 & 1 \\ -2 & - \delta \end{bmatrix}$$ これらの行列の固有値を求めて、$\delta$によって変化する実部を見れば、固定点の安定性を知ることができる。動力学は多くのシステムを扱うが、その解析研究はこの伝統的な方法から大きく逸脱することはほとんどない。