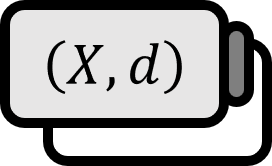📂距離空間

距離空間における数列の収束

定義¹

$\left\{ p_{n} \right\}$が距離空間 $(X,d)$の点の列であるとしよう。以下の条件を満たす点 $p \in X$が存在するなら、列 $\left\{ p_{n} \right\}$は$p$に収束する^convergeと言い、$p_{n} \rightarrow p$または$\lim \limits_{n\to \infty}p_{n}=p$と表される。

$$ \forall \varepsilon >0,\ \exists N\in \mathbb{N}\ \mathrm{s.t}\ n\ge N \implies d(p_{n},p)<\varepsilon $$

$\left\{ p_{n} \right\}$が収束しないなら発散する^divergeと言う。また、すべての$p_{n}$の集合を$\left\{ p_{n} \right\}$の値域^rangeと言う。$\left\{ p_{n} \right\}$の値域が有界なら、列$\left\{ p_{n} \right\}$は有界^boundedだと言われる。

定理

$\left\{ p_{n} \right\}$を距離空間$(X,d)$の列とする。

(a) $p_{n}\to p$の必要十分条件は、すべての$p$の近傍が無限個を除くすべての$\left\{ p_{n} \right\}$の項を含むことである。

(b) $p_{n} \to p$であり、かつ$p_{n} \to p^{\prime}$ならば、$p=p^{\prime}$である。

(c) $\left\{ p_{n} \right\}$が収束すれば、有界である。

(d) $E\subset X$が与えられたとしよう。$p$が$E$の集積点であれば、$p=\lim \limits_{n \to \infty}p_{n}$を満たす$E$の列$\left\{ p_{n} \right\}$が存在する。また、$\left\{ p_{n} \right\}$が異なる点の集合であれば、逆も成り立つ。

証明

(a)

• $(\implies)$

  $p_{n} \to p$と仮定しよう。任意の正の数$\varepsilon >0$が与えられたとする。$V$を$p$の半径が$\varepsilon$の近傍とする。近傍の定義により、次が成り立つ。

  $$ d(p,q)<\varepsilon\quad \implies q\in V $$

  しかし、仮定により、与えられた$\varepsilon$に対して、以下の条件を満たす$N$が存在する。

  $$ \forall n \ge N,\ d(p_{n},p) <\varepsilon $$

  従って、有限個の点を除くすべての$p_{n}$が$V$に含まれる。

• $(\impliedby)$

  $p$のすべての近傍が無限個を除くすべての$\left\{ p_{n} \right\}$を含むと仮定しよう。任意の正の数$\varepsilon>0$が与えられたとする。$V$を$p$の半径が$\varepsilon$の近傍とする。すると、仮定により、以下の条件を満たす$N$が存在する。

  $$ n \ge N \implies p_{n}\in V $$

  なので、$V$は$p$の近傍なので、次が成り立つ。

  $$ \forall n \ge N,\quad d(p_{n},p)<\varepsilon $$

  従って、$p_{n}\to p$。

■

(b)

任意の正の数$\varepsilon >0$が与えられたとしよう。仮定により、以下の条件を満たす2つの正の数$N$、$N^{\prime}$が存在する。

$$ \begin{align*} n\ge N & \implies d(p_{n},p) <\frac{\varepsilon}{2} \\ n\ge N^{\prime} & \implies d(p_{n},p) <\frac{\varepsilon}{2} \end{align*} $$

すると、$n \ge \max(N,N^{\prime})$に対して、以下の式が成り立つ。

$$ d(p,p^{\prime}) \le d(p,p_{n}) + d(p_{n},p^{\prime})<\varepsilon $$

$\varepsilon$は任意の正の数なので、

$$ d(p,p^{\prime})=0 $$

であり、距離の定義により、$p=p^{\prime}$

■

(c)

$\left\{ p_{n} \right\}$が$p$に収束すると仮定しよう。仮定により、以下の式が成り立つ正の数$N$が存在する。

$$ n \ge N \implies d(p_{n},p)<1 $$

今、

$$ r=\max \left\{ 1,\ d(p_{1},p),\ \cdots,\ d(p_{N},p) \right\} $$

としよう。すると、すべての$n$に対して、

$$ d(p_{n},p)\le r $$

なので、$\left\{ p_{n} \right\}$は有界である。

■

(d)

• $(\implies)$

  $E\subset X$であり、かつ、$p$が$E$の集積点であるとしよう。集積点の定義により、各$n$に対して、

  $$ d(p_{n},p) < \frac{1}{n} $$

  を満たす$p_{n}\in E$が存在する。今、任意の正の数$\varepsilon >0$と$N\varepsilon>1$を満たす$N$が与えられたとする。すると、$ n >N$に対して、次が成り立つ。

  $$ d(p_{n},p)< \frac{1}{n}<\frac{N}{n}\varepsilon<\varepsilon $$

  従って、$\left\{ p_{n} \right\}$は$p$に収束する。

• $(\impliedby)$

  $p=\lim \limits_{n\to\infty}p_{n}$を満たす$E$の異なる点の列$\left\{ p_{n} \right\}$が存在すると仮定しよう。すると、すべての正の数$\varepsilon >0$に対して、

  $$ n \ge N \implies d(p_{n},p)< \varepsilon $$

  を満たす$N$が存在する。この時、$V_{\varepsilon}$を$p$の半径が$\varepsilon$の近傍とする。すると、$V_{\varepsilon}$は$p$ではない$p_{n} \in E (n\ge N)$を含むので、$p$は$E$の集積点である。

■