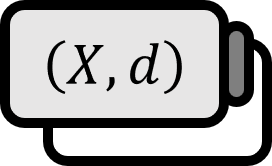距離空間における開集合と閉集合の性質
$(X,d)$が距離空間だとする。$p \in X$であり、$E \subset X$とする。
$d(q,p)<r$を満たす全ての$q$を含む集合を点$p$の近傍neighborhoodと定義し、$N_{r}(p)$と表記する。この時、$r$を$N_{r}(p)$の半径と呼ぶ。距離を省略できる場合は$N_{p}$のようにも表記される。
$p$の全ての近傍が$q\ne p$であり$q\in E$の$q$を含む場合、$p$を$E$の集積点limit pointと呼ぶ。
$E$の全ての集積点が$E$に含まれる場合、$E$が閉じているclosedと言う。
$N\subset E$を満たす$p$の近傍$N$が存在するなら、$p$を$E$の内点interior pointと呼ぶ。
$E$の全ての点が$E$の内点である場合、$E$が開いているopenと言う。
定理
距離空間$X$で、開いた集合のコレクション1を$\left\{ O_{\alpha} \right\}$、閉じた集合のコレクションを$\left\{ C_{\alpha} \right\}$としよう。そうすると
(a) 開いた集合の合併$\bigcup_{\alpha} O_{\alpha}$もまた開いた集合だ。
(b) 閉じた集合の共通部分$\bigcap_{\alpha} C_{\alpha}$もまた閉じた集合だ。
(c) 開いた集合の有限の共通部分$\bigcap_{i=1}^{n}O_{i}$もまた開いた集合だ。
(d) 閉じた集合の有限の合併$\bigcup _{i=1}^{n} C_{i}$もまた閉じた集合だ。
$(c)$、$(d)$で有限という条件がなければ成立しない。これは反例を通して示すことができる。
証明
(a)
$O=\bigcup_{\alpha} O_{\alpha}$とする。$p \in O$ならば、何らかの$\alpha$について$p \in O_{\alpha}$である。従って、開いた集合の定義により、$p$は$O_{\alpha}$の内点だ。また、内点の定義により、$p$は$O$の内点となる。任意の$p\in O$について、$p$が$O$の内点であるため、$O$は開いた集合だ。
■
(b)
ド・モルガンの定理 $\left\{ E_{\alpha}\right\}$を集合$E_{\alpha}$のコレクションとする。すると下記の式が成立する。 $$ \left( \bigcup \limits_{\alpha}E_{\alpha} \right)^{c}=\bigcap \limits_{\alpha} (E_{\alpha})^{c} $$
証明は下に紹介する。
ド・モルガンの定理によって、次が成立する。
$$ \left( \bigcap_{\alpha} C_{\alpha} \right)^{c}=\bigcup_{\alpha}(C_{\alpha})^{c} \tag{1} $$
$C_{\alpha}$が閉じた集合なので、$(C_{\alpha})^{c}$は開いた集合だ。それにより、(a) によって$\bigcup_{\alpha}(C_{\alpha})^{c}=\left( \bigcap_{\alpha} C_{\alpha} \right)^{c}$は開いた集合だ。従って、$\bigcap_{\alpha} C_{\alpha}$は開いた集合の補集合なので閉じた集合だ。
■
(c)
$O=\bigcap_{i=1}^{n}O_{i}$とする。すると、任意の点$p\in O$について、全ての$i$に対して$p\in O_{i}\ (i=1,\cdots,n)$が成立する。従って、開いた集合と内点の定義により、それぞれの$i$に対して
$$ N_{i} \subset O_{i} \quad (i=1,\cdots,n) $$
を満たす半径が$r_{i}$の$p$の近傍が存在する。この時$r=\min (r_{1},\cdots,r_{n})$としよう。そして$N=N_{r}(p)$とする。そのため、$N$は最も小さい半径を持つ近傍なので、次が成立する。
$$ N\subset O_{i} \quad (i=1,\cdots,n) $$
よって、$N \subset O$が成立し、内点の定義により、$p$は$O$の内点だ。任意の$p\in O$について、$p$は常に$O$の内点なので、$O$は開いた集合だ。
■
(d)
ド・モルガンの定理によって、次が成立する。
$$ \left( \bigcup_{i=1}^{n}C_{i} \right)^{c} = \bigcap _{i=1}^{n} (C_{i})^{c} $$
$C_{i}$が閉じているため、補助定理2により$(C_{i})^{c}$は開いている。それにより、$(c)$によって$\bigcap_{i=1}^{n}(C_{i})^{c}=\left( \bigcup _{i=1}^{n}C_{i} \right)^{c}$は開いた集合だ。それで、再び補助定理2によって、$\bigcup _{i=1}^{n}C_{i}$は閉じた集合だ。
■
ド・モルガンの定理の証明
part 1. $\left( \bigcup \limits_{\alpha}E_{\alpha} \right)^{c} \subset \bigcap \limits_{\alpha} (E_{\alpha})^{c}$
$x\in \left( \bigcup \limits_{\alpha}E_{\alpha} \right)^{c}$とする。すると、補集合の定義により、次が成立する。
$$ \begin{align*} && x &\notin \bigcup \limits_{\alpha}E_{\alpha} \\ \implies&& x&\notin E_{\alpha}\quad &\forall \alpha \\ \implies&& x&\in(E_{\alpha})^{c}\quad &\forall \alpha \\ \implies&& x&\in \bigcap\limits_{\alpha}(E_{\alpha})^{c} \end{align*} $$
よって
$$ \left( \bigcup \limits_{\alpha}E_{\alpha} \right)^{c} \subset \bigcap \limits_{\alpha} (E_{\alpha})^{c} $$
part 2. $\left( \bigcup \limits_{\alpha}E_{\alpha} \right)^{c} \supset \bigcap \limits_{\alpha} (E_{\alpha})^{c}$
$x\in \bigcap \limits_{\alpha} (E_{\alpha})^{c}$とする。すると、次が成立する。
$$ \begin{align*} && x &\in (E_{\alpha})^{c} &\forall \alpha \\ \implies && x &\notin E_{\alpha} &\forall \alpha \\ \implies&& x&\notin \bigcup \limits_{\alpha}E_{\alpha} \\ \implies && x &\in \left( \bigcup \limits_{\alpha} E_{\alpha} \right)^{c} \end{align*} $$
よって
$$ \left( \bigcup \limits_{\alpha}E_{\alpha} \right)^{c} \supset \bigcap \limits_{\alpha} (E_{\alpha})^{c} $$
■
集合の集まりの意味だ。 ↩︎