📂Banach Space

Proof of Riesz's Lemma

Theorem¹

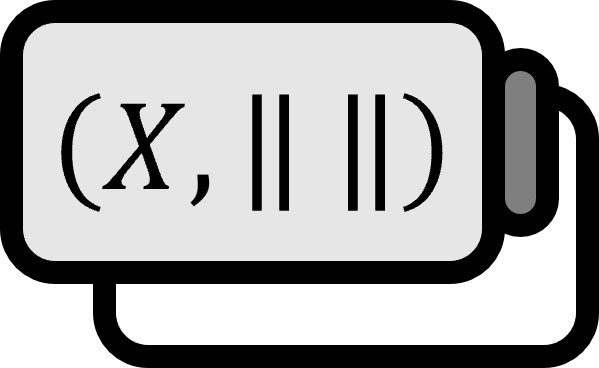
For a subspace $Y \subsetneq X$ of a normed space $(X , \| \cdot \| )$, suppose that $Y$ is a closed set. Then for every $\theta \in (0,1)$ and $y \in Y$, there exists $x_{\theta} \in X$ satisfying $\| x_{ \theta } \| = 1$ and $\| x_{ \theta } - y \| > \theta$.

Proof

Strategy: We show that a concrete $x_{\theta}$ exists, and then show that $\| x_{ \theta } - y \| > \theta$ holds.

---

For $x_{0}$ with $ x_{0 } \notin Y$ and $ x_{0 } \in X$, let $d:= \inf \left\{ \| x_{0} - y \| : y \in Y \right\}$. Suppose that $d=0$; then there exists a sequence $\left\{ y_{n} \right\}_{n \in \mathbb{N} }$ in $Y$ satisfying $\displaystyle \lim_{ n \to \infty } \| x_{0} - y_{n} \| = 0$. This means that $x_{0} \in \overline{Y}$, but since $\overline{Y} = Y$, we get $x_{0} \in Y$, which is a contradiction, so it must be that $d> 0$.

Now, there exists $y_{0} \in Y$ satisfying $\displaystyle 0 < \| x_{0} - y_{0} \| < {{d} \over {\theta }}$, farther than the distance $d$ between $x_{0}$ and the boundary of $\overline{Y}$. For this $\theta$, let $\displaystyle x_{ \theta } := {{ x_{0} - y_{0} } \over { \| x_{0} - y_{0} \| }}$. If $y \in Y$, then

$$ \| x_{ \theta} - y \| = \left\| {{ x_{0} - y_{0} } \over { \| x_{0} - y_{0} \| }} - y \right\| = {{1 } \over { \| x_{0} - y_{0} \| }} \left\| x_{0} - y_{0} - \| x_{0} - y_{0} \| y \right\| $$

Since $(y_{0} + \| x_{0} - y_{0} \| y) \in Y$ and $\left\| x_{0} - y_{0} - \| x_{0} - y_{0} \| y \right\| \ge d$,

$$ \| x_{ \theta} - y \| \ge {{1 } \over { \| x_{0} - y_{0} \| }} d $$

Since $\displaystyle \| x_{0} - y_{0} \| < {{d} \over {\theta }}$, the following holds.

$$ \| x_{ \theta} - y \| > {{ \theta } \over {d }} d = \theta $$

■