Banach Space
Definition1
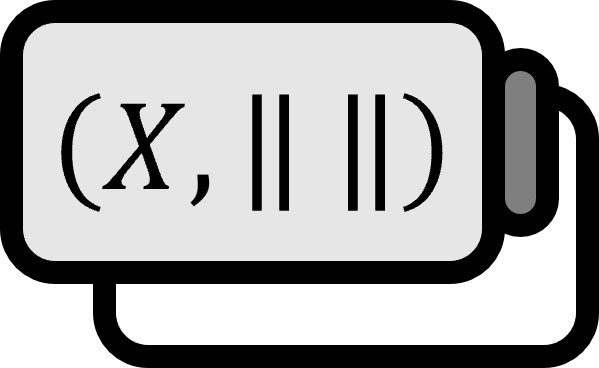
A Banach space is a complete normed space.
Explanation
A complete space refers to a space in which every Cauchy sequence converges.
Banach space is a space that satisfies all of the following conditions, making it an extremely useful space as it is defined with a distance function and possesses completeness:
- It is a vector space.
- It is a normed space. $\implies$ It is a metric space.
- It is a complete space.
Moreover, as an example of Banach spaces, one can think of the set of continuous functions defined on a closed interval. This serves as a very simple example while also underpinning various important theorems, making it a very important fact. Examples of Banach spaces include:
- $C[a,b]$
- $\R^{n}$
- $\mathbb{C}^{n}$
An introduction to the proof for $C[a,b]$ is as follows.
Proof 1
Part 1. Vector Space
Continuous functions defined on a closed interval have a constant function $f(x) = 0$ as an identity element and $f(x) = - f(x)$ as an inverse element. Besides, $C[a,b]$ well satisfies the conditions of a vector space over the scalar field $\mathbb{R}$.
Part 2. Normed Space
Defining $\| \cdot \|$ for $f \in C [a,b]$ as $\displaystyle \| f \| := \sup_{ a \le t \le b } | f (t) |$ satisfies the conditions for a norm.
Part 3. Completeness
Let’s consider $\left\{ f_{n} \right\}_{n \in \mathbb{N}}$ as a Cauchy sequence under $C [a,b]$. In other words, for all $\varepsilon / 3 > 0$, there exists $N_{1} \in \mathbb{N}$ that satisfies $\| f_{n} (t) - f_{m} (t) \| < \varepsilon / 3$ whenever $n,m > N_{1}$.
Since $\mathbb{R}$ is a complete space, for any fixed $t_{0} \in [a,b]$, $\displaystyle \lim_{n \to \infty} f_{n} (t_{0})$ can be expressed with respect to some $f : [a,b] \to \mathbb{R}$ as
$$ \lim_{n \to \infty} f_{n} ( t_{0} ) = f ( t_{0} ) $$
Then, since $f_{n}$ is a Cauchy sequence, for any $t \in [a,b]$, there exists $N_{2}$ that satisfies
$$ \begin{align*} | f(t) - f_{m} (t) | =& \left| \lim_{n \to \infty} f_{n} (t) - f_{m} (t) \right| \\ =& \lim_{n \to \infty} | f_{n} (t) - f_{m} (t) | \\ \le & \lim_{n \to \infty} \sup_{t \in [a,b] } | f_{n} (t) - f_{m} (t) | \\ =& \lim_{n \to \infty} \| f_{n} - f_{m} \| \\ <& \varepsilon / 3 \end{align*} $$
when $m \ge N_{2}$. Of course, there is still no guarantee that the function $f$ is continuous, but merely that it is defined to have a value converging eventually for all $t \in [a,b]$ as the function value. However, from this definition, it can be guaranteed that $f_{n}$ uniformly converges to $f$, meaning that for all $x,y \in [a,b]$ and $\varepsilon / 3 > 0$, there exists $N_{3} \in \mathbb{N}$ satisfying both simultaneously when $n \ge N_{3}$.
$$ \left| f_{n} (x) - f(x) \right| < \varepsilon / 3 \\ \left| f_{n} (y) - f(y) \right| < \varepsilon / 3 $$
Now, it remains to show that $f$ is a continuous function.
Let’s consider $E \subset \mathbb{R}$ as not an empty set.
If $f$ is continuous and $E$ is a bounded closed interval, then $f$ is uniformly continuous.
Since $f_{n} : [a,b] \to \mathbb{R}$ is continuous and $[a,b] \subset \mathbb{R}$ is compact, $f_{n}$ is uniformly continuous in $[a,b]$. That is, for all $x,y \in [a,b]$ and $\varepsilon / 3 > 0$, there exists $\delta > 0$ satisfying
$$ \left| f_{n}(x) - f_{n}(y) \right| < \varepsilon / 3 $$
when $|x-y| < \delta$.
Combining the above results, since there exists $\delta > 0$ and $N_{3} \in \mathbb{N}$ satisfying both
$$ \begin{align*} |f(x) - f(y)| \le & \left| f (x) - f_{n} (x) \right| + \left| f_{n}(x) - f_{n}(y) \right| + \left| f_{n} (y) - f(y) \right| \\ =& \varepsilon / 3 + \varepsilon / 3 + \varepsilon / 3 \\ =& \varepsilon \end{align*} $$
when $|x-y| < \delta$ and $n \ge N_{3}$, $f$ is uniformly continuous in $[a,b]$ and converges to $f \in C[a,b]$. Hence, any Cauchy sequence of continuous functions $\left\{ f_{n} \right\}_{n \in \mathbb{N}}$ uniformly converges to some $f \in C[a,b]$, proving that $C[a,b]$ possesses completeness.
■