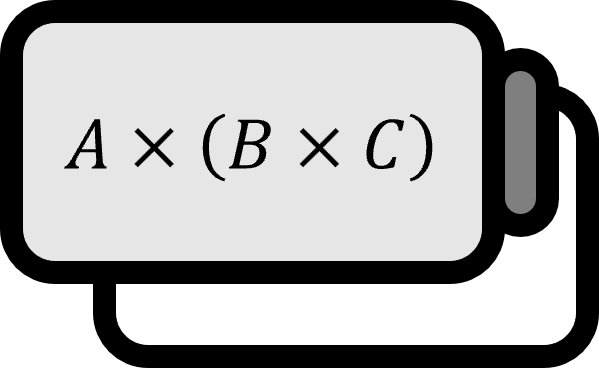What is a Pseudovector?
Description
Studying physics, one might come across the term pseudovector or axial vector. The tricky part is that you might encounter pseudovectors without really knowing what they are. It is said that one can study undergraduate physics without understanding pseudovectors, but I’ve never seen a textbook that explains it properly. I first encountered pseudovectors as Pseudovectors in a problem in Griffith’s electromagnetism. However, just solving problems was not enough to grasp what a pseudovector is. A detailed textual explanation would have been more beneficial. The term comes from $\mathrm{Pseudo\ vector}$, which is why it is also called a pseudovector or axial vector. $\mathrm{Pseudo}$ means ‘false, fake’. In other words, it is not a real vector but something similar yet slightly different.
A pseudovector, during a symmetry transformation, is a vector whose components along the axis of transformation do not change sign, while the components perpendicular to it do.
Putting it this way might not make it clearer. Simply put, during a symmetry transformation regarding the $xy$ plane, $x$, $y$ components reverse their sign while the $z$ component does not. When the symmetry transformation is done regarding the origin, none of the components change their sign. Such vectors that satisfy these characteristics are referred to as pseudovectors. The most typical example is the cross product of two vectors. Therefore, physical quantities represented by the cross product, like angular momentum and torque, are all pseudovectors. The following image makes it easier to understand, but the cross product of two vectors does not move normally with respect to symmetry transformation.

Vectors we know transform in symmetry as shown in the image above. When a symmetry transformation against the $xy$ plane is performed, the $z$ component changes its sign. Vectors satisfy these properties and can be called vectors only if they satisfy these properties. However, the cross product of two vectors does not satisfy these properties. Although the cross product is also a vector, the outcome of the cross product before and after symmetry transformation differs.

Let’s use ${}^{\prime}$ to mean a vector that has been symmetry transformed regarding the $xy$ plane. Then, as you can see from the above image, it results in $(\mathbf{A} \times \mathbf{B})^{\prime} \ne \mathbf{A}^{\prime} \times \mathbf{B}^{\prime}$. When performing a symmetry movement based on the $xy$ plane, only the sign of $z$ should change, but instead, the $z$ sign remains the same, and the $x$, $y$ signs reverse. A direct comparison through calculation is as follows.
Symmetry regarding the $xy$ plane
| Before Symmetry | After Symmetry | Remarks |
|---|---|---|
| $\mathbf{A}=(1,1,1)$ | $\mathbf{a}^{\prime}=(1,1,-1)$ | $x$, $y$ component sign unchanged$z$ component sign reversed |
| $\mathbf{B}=(2,4,3)$ | $\mathbf{B}’=(2,4,-3)$ | $x$, $y$ component sign unchanged$z$ component sign reversed |
| $\mathbf{A}\times \mathbf{B}=(-1,-1,2)$ | $\mathbf{a}^{\prime}\times \mathbf{B}’=(1,1,2)$ | $x$, $y$ component sign reversed$z$ component sign unchanged |
Symmetry regarding the Origin
| Before Symmetry | After Symmetry | Remarks |
|---|---|---|
| $\mathbf{A}=(1,1,1)$ | $\mathbf{a}^{\prime}=(-1,-1,-1)$ | $x$, $y$, $z$ component signs reversed |
| $\mathbf{B}=(2,4,3)$ | $\mathbf{B}’=(-2,-4,-3)$ | $x$, $y$, $z$ component signs reversed |
| $\mathbf{A}\times \mathbf{B}=(-1,-1,2)$ | $\mathbf{a}^{\prime}\times \mathbf{B}’=(-1,-1,2)$ | $x$, $y$, $z$ component signs unchanged |