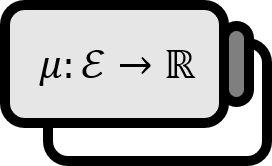📂Measure Theory

Exterior Measure

Definition ¹

Given $E \subset \mathbb{R}$, $\left\{ I_{n} \in \mathcal{I} \ | \ n \in \mathbb{N} \right\}$, $\left\{ E_{n} \in \mathscr{P} ( \mathbb{R} ) \ | \ n \in \mathbb{N} \right\}$, we define the function $m^{ \ast } (E) : = \inf Z_{E}$ as an Outer Measure.

Fundamental Properties

The outer measure has the following properties:

• [1] Generalization of Length: $I \in \mathcal{I} \implies m^{ \ast } (I) = l(I)$
• [2] Non-Negativity: $N \in \mathcal{N} \iff m^{ \ast }(N) = 0$
• [3] Monotonicity: $E_{1} \subset E_{2} \implies m^{ \ast }(E_{1}) \le m^{ \ast }(E_{2})$
• [4] Invariance under Transformation: $t \in \mathbb{R} \implies m^{ \ast } (E) = m^{ \ast } (E+t)$
• [5] Countable Subadditivity: $\displaystyle m^{ \ast } \left( \bigcup_{n=1}^{\infty} E_{n} \right) \le \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$

Explanation

Since the elements of $Z_{E}$ sum up the distances, it is evident that $Z_{E}$ is bounded below and the existence of $\inf Z_{E}$ is trivial. The condition requires satisfaction of $\displaystyle E \subset \bigcup_{n=1}^{\infty} I_{n}$, and choosing the smallest $\inf$ can be thought of as ’narrowing down from the outside.’ Therefore, the outer measure is also referred to as the (Lebesgue) Exterior Measure, and this naming is considered to be valid.

As can be guessed from property [1], the outer measure is a concept devised for generalizing ’length.’ Naturally, it should cover the lengths we have intuitively and conventionally used. In this sense, properties [2]~[5] are obligatory, and without them, it could hardly be called a generalization.

Particularly in [5], it mirrors the triangle inequality of norms with the difference that the number of terms is countably infinite. Common sensically, if for all $i \ne j$ and when $E_{i} \cap E_{j} = \emptyset$, $$m^{ \ast } \left( \bigcup_{n=1}^{\infty} E_{n} \right) = \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$$ holds, i.e., if $\displaystyle m^{ \ast } \left( \bigsqcup_{n=1}^{\infty} E_{n} \right) = \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$ is true, then the generalization of length can be considered successful. (Here, $\bigsqcup$ denotes the symbol for the union of mutually disjoint sets.)

Limitations of the Outer Measure

The issue is even with such strong conditions set, there’s an “abnormal” counterexample that fails to satisfy the equation. To satisfy this equality, mathematicians, including Lebesgue, have sought out new conditions.

Counterexample

For all $i \ne j$, the following does not always hold: $$\displaystyle E_{i} \cap E_{j} = \emptyset \implies m^{ \ast } \left( \bigsqcup_{n=1}^{\infty} E_{n} \right) = \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$$

Disproof

Providing a counterexample for $\displaystyle E_{i} \cap E_{j} = \emptyset \implies m^{ \ast } \left( \bigsqcup_{n=1}^{\infty} E_{n} \right) \ne \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$ is sufficient.

---

Defining the relation where if $x,y \in [0,1]$ and $y-x \in \mathbb{Q}$, then $x \sim y$, we can easily show that $\sim$ is an equivalence relation. $\sim$ determines the equivalence class $A_{\alpha}$, and since $[0,1]$ is uncountable, for all $\alpha \in [0,1]$, an $A_{\alpha}$ exists, making $A_{\alpha}$ uncountably many. Meanwhile, each $A_{\alpha}$ is a countable set due to $x \in A_{\alpha}$ and $q \in \mathbb{Q} \cap [0,1]$ being true for $x - (x - q) = q \in \mathbb{Q}$.

Now, consider the set $E$ gathered by picking one element from all $A_{\alpha}$. The construction of such a set $E$ is guaranteed by the Axiom of Choice.

Then for any given $q_{n} \in \mathbb{Q} \cap [0,1]$, we can define $E_{n} := E + q_{n}$. Assuming $z \in E_{i} \cap E_{j}$, $$a_{\alpha} + q_{i} = z = a_{\beta} + q_{j} \\ a_{\alpha} - a_{\beta} = q_{j} - q_{i} \in \mathbb{Q}$$ implies $a_{\alpha} - a_{\beta} \in \mathbb{Q}$, and means $a_{\alpha}$ and $a_{\beta}$ belong to some $A_{\lambda}$ simultaneously. However, since $E$ includes only one element from each $A_{\alpha}$, this is a contradiction, and thus for $i \ne j$, $E_{i} \cap E_{j} = \emptyset$ must hold.

Since $\displaystyle [0,1] \subset \bigsqcup_{n=1}^{\infty} E_{n} \subset [-1,2]$, by [3] Monotonicity, $$m^{ \ast } [0,1] \le m^{ \ast } \left( \bigsqcup_{n=1}^{\infty} E_{n} \right) \le m^{ \ast } [-1, 2]$$ If we assume $\displaystyle m^{ \ast } \left( \bigsqcup_{n=1}^{\infty} E_{n} \right) = \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$, $$1 \le \sum_{n=1}^{\infty} m^{ \ast } ( E_{n} ) \le 3$$

By [4] Invariance under Transformation, since $m^{ \ast }(E_{n}) = m^{ \ast }(E + q_{n}) = m^{ \ast }(E)$, $$1 \le \sum_{n=1}^{\infty} m^{ \ast } ( E_{n} ) = m^{ \ast } (E) + m^{ \ast } (E) + \cdots \le 3$$ For $\displaystyle 1 \le \sum_{n=1}^{\infty} m^{ \ast } ( E )$ to hold, $\displaystyle \sum_{n=1}^{\infty} m^{ \ast } ( E ) = \infty$ must, and for $\displaystyle \sum_{n=1}^{\infty} m^{ \ast } ( E ) \le 3$ to occur, $\displaystyle \sum_{n=1}^{\infty} m^{ \ast } ( E ) = 0$ must. Satisfying both conditions simultaneously is impossible, therefore, $$m^{ \ast } \left( \bigsqcup_{n=1}^{\infty} E_{n} \right) \ne \sum_{n=1}^{\infty} m^{ \ast } (E_{n})$$

■

It’s not just the counterexample itself, but the fact that a brain capable of conceiving such a counterexample exists in the world is even more shocking. If you’ve discovered a counterexample that’s not similar and is original, it’s recommended to visit either a psychiatric hospital or graduate school.