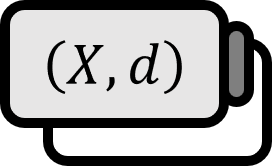Inner Enclosure Boundary in Metric Spaces
Definition
Let’s say $\left( X, d \right)$ for a metric space.
When there exists an open set $O$ that satisfies $x \in O \subset A$, $x$ is called an Interior Point of $A$.
The set of interior points of $A$, $A^{\circ}$, is called the Interior of $A$.
The union $\overline{A} : = A \cup a '$ of $A$ and its codomain is called the Closure of $A$.
When it’s both $x \in \overline{A}$ and $x \in \overline{X \setminus A}$, $x$ is called a Boundary Point of $A$.
$\partial A : = \overline{A} \cap \overline{X \setminus A}$ is called the Boundary of $A$.
Explanation
Though it might not be essential to define, the set outside of $\overline{A}$ in contrast to the interior is called the Exterior.
The open set and these concepts can be defined differently but are essentially the same.
These definitions are such that anyone can understand them if they read them carefully. Let’s quickly grasp them through diagrams.
$$ A $$

Consider these concepts when the given set is as above.
$$ A^{\circ} $$

The Interior is the largest open subset of $X$ that is contained within $A$.
$$ \overline{A} $$

The Closure is the smallest closed subset of $X$ that contains $A$.
$$ \partial A $$

The Boundary can be seen as a subset of $X$ that is the Closure minus the Interior.
While distinguishing between the Interior and Closure is not particularly difficult, the Boundary might be confusing at first glance, depending on whether it’s a dotted or solid line. If it’s a border, just consider it as the Boundary, no ifs or buts.
Through such definitions, the following properties can essentially be seen as the definitions of open and closed sets.
Properties: Open and Closed Sets
Let’s say $A$ is a subset of the metric space $X$.
$A$ being an open set is equivalent to $A = A^{\circ}$.
$A$ being a closed set is equivalent to $A = \overline{A}$.
Of course, these properties can be proven, but it’s perfectly fine to accept them as facts.