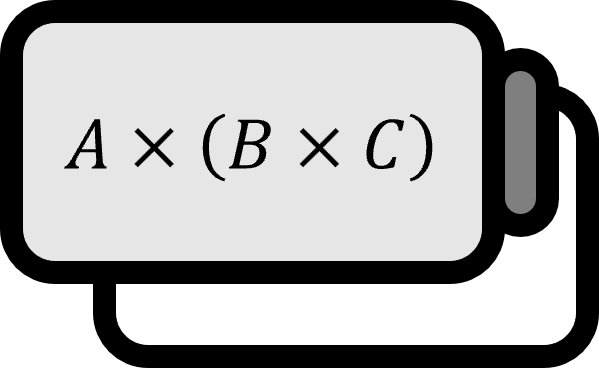Coordinate Systems and Coordinates in Physics
Definition
When each pair of $n$-ordered pairs $(a_{1}, a_{2}, \dots, a_{n})$ uniquely determines a point in a $n$-dimensional space, the set of these $n$-ordered pairs is called a ($n$-dimensional) coordinate system, and the element $(a_{1}, a_{2}, \dots, a_{n})$ of the coordinate system is called the coordinate of that point.
Description
In physics, it is generally $n \le 4$.
The above definition is nothing more than a reorganization of concepts that have been used naturally from high school. The important point is that the coordinate must uniquely determine a single point. Given a coordinate $(a_{1}, \dots, a_{n})$, the point in space it signifies must be unique. However, conversely, when a point in space is given, the coordinate $(a_{1}, \dots, a_{n})$ representing it may not be unique. In particular, coordinate systems that use angles can have multiple representations of coordinates at points on the axis or at the origin due to trigonometric functions.
Coordinate System
- $\mathbb{R}$ represents the set of real numbers.
- $\mathbb{R}^{n} = \overbrace{\mathbb{R} \times \cdots \times \mathbb{R}}^{n}$ represents a $n$-dimensional space.
A number line is a 1-dimensional coordinate system.
Cartesian Coordinate System
The most closely related and intuitive coordinate system in everyday life. In physics, the 2-dimensional Cartesian coordinate system, coordinate plane, and the 3-dimensional Cartesian coordinate system, coordinate space, are mainly discussed. The coordinates of a 3-dimensional Cartesian coordinate system are expressed as follows: $$ (x, y, z) \in \mathbb{R} \times \mathbb{R} \times \mathbb{R} = \mathbb{R}^{3} $$ Hence, instead of Cartesian coordinate system, it is also referred to as a $(x, y, z)$-coordinate system. This convention is applied in the following coordinate systems as well.
Referring to the Cartesian coordinate system as the orthogonal coordinate system is considered incorrect because not only the Cartesian coordinate system but also polar, spherical, and cylindrical coordinate systems all have axes that are orthogonal to each other. The orthogonal coordinate system is a larger concept that includes the Cartesian coordinate system.
Polar Coordinate System
The polar coordinate system is convenient for describing radially symmetric motion in 2 dimensions. It determines a point in 2-dimensional space by the distance $r$ from the origin and the angle $\theta$ from the $x$-axis. $$ (r,\theta) \in [0, \infty) \times [0, 2\pi) $$ The coordinates of the origin are not unique. The following holds for different $\theta_{1}, \theta_{2}$: $$ (0, \theta_{1}) = (0, \theta_{2}) $$
Cylindrical Coordinate System
A point in 3-dimensional space is represented by the length $\rho$ (or $s$) projected onto the $xy$-plane, the angle $\phi$ from the $x$-axis, and the $z$-coordinate. $$ (\rho, \phi, z) \in [0, \infty) \times [0, 2\pi) \times \mathbb{R} $$ The coordinates of the origin are not unique. The following holds for different $\phi_{1}, \phi_{2}$: $$ (0, \phi_{1}, 0) = (0, \phi_{2}, 0) $$ The coordinates on the $z-$ axis are also not unique. The following holds for different $\phi_{1}, \phi_{2}$: $$ (0, \phi_{1}, z) = (0, \phi_{2}, z) $$
Spherical Coordinate System
Convenient for describing radially symmetric motion in 3-dimensional space. It is an extension of the polar coordinate system to 3 dimensions. A point in 3-dimensional space is determined by the distance $r$ from the origin, the polar angle $\theta$, and the azimuthal angle $\phi$. $$ (r, \theta, \phi) \in [0, \infty) \times [0, \pi] \times [0, 2\pi) $$ Similar to the cylindrical coordinate system, the coordinates of the origin and points on the $z$-axis are not unique.
The use of $\theta$ and $\phi$ interchangeably is sometimes practiced, but I think such notation is inappropriate. Thinking about the meaning, and considering the international standards defined by ISO, $(r, \theta, \phi)$ is preferred. Moreover, according to Wikipedia, US math textbooks use $(r, \phi, \theta)$ notation, but considering the irrationality of the US customary units, including the yard-pound system, it’s worth reflecting on.