📂Functions

Composition of Functions

Definitions

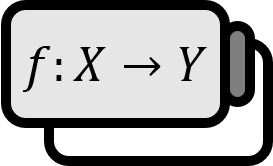
A function $f: X \to Y$, $g: f(X) \to Z$ is defined as follows: the composition of $g$ with $f$ is called $h: X \to Z$, and it is denoted by $h=g \circ f$.

$$h(x) = (g\circ f) (x) := g\left( f(x) \right)$$