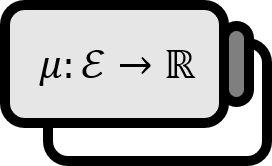📂Measure Theory

Regular Measure

Definition: Regularity of a Measure ¹

Let $\mu$ be a measure defined on a measurable space $(X, \Sigma)$.

1. A measurable set $A \in \Sigma$ is said to be Inner Regular if it satisfies the following: $$\mu (A) = \sup \left\{ \mu (F) : F \subset A, F \in \Sigma \text{ is compact} \right\}$$
2. A measurable set $A \in \Sigma$ is said to be Outer Regular if it satisfies the following: $$\mu (A) = \inf \left\{ \mu (G) : G \supset A, G \in \Sigma \text{ is open} \right\}$$
3. If all measurable sets $A \in \Sigma$ are Inner Regular with respect to $\mu$, then $\mu$ is called an Inner Regular Measure.
4. If all measurable sets $A \in \Sigma$ are Outer Regular with respect to $\mu$, then $\mu$ is called an Outer Regular Measure.
5. If $\mu$ is both Inner Regular and Outer Regular, it is referred to as a Regular Measure.

Description

As one might infer from the inclusion of compactness in the definition, a regular measure is mentioned as a ‘rather nice’ measure along with the condition of being a Borel measure. Without delving into the abyss of measure theory, the notion of regularity serves more to prevent all sorts of pathological counterexamples that might arise in the development of theory rather than playing an explicit role itself.