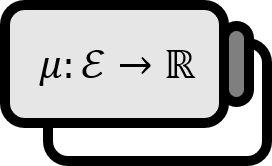📂Measure Theory

Positive Set, Negative Set, Null Set

Definition¹

Let us call $\nu$ on $(X,\mathcal{E})$ a sign measure. And let us denote $E,F \in \mathcal{E}$. Then

• When $\nu (F) \ge 0,\ \forall F\subset E$, we call $E$ regarding $\nu$ a positive set or simply positive.

• When $\nu (F) \le 0,\ \forall F\subset E$, we call $E$ regarding $\nu$ a negative set or simply negative.

• When $\nu (F)=0,\ \forall F\subset E$, we call $E$ regarding $\nu$ a null set or $\nu$-null.

Explanation

According to the definition, the null set is a set that is both a positive set and a negative set at the same time. It’s easy to misunderstand the definitions of positive set and negative set, so it’s crucial to understand them correctly. $E$ is not called a positive set when $\mu (E)>0$. For $E$ to be called a positive set, for every measurable subset $F\in\mathcal{E}$ of it, $\mu (F) \ge 0$ must be satisfied. Naturally, this condition implies that $\nu (E) >0$ holds. To summarize:

$$E\ \mathrm{is\ positive\ set\ for\ }\nu \implies \nu (E)>0 \\ \nu (E)>0 \not\implies E\ \mathrm{is\ positive\ set\ for\ }\nu$$

The same applies to negative sets and null sets. The above discussion is only applicable to sign measures. The case is a bit different for absolute measures. When $\mu$ is called an absolute measure, since it always has a function value greater or equal to $0$, $\mu (E)=0$ being equal to $E$ being $\nu$-null are equivalent. The same goes for discussions about positive sets. Therefore, there’s no need to specifically use the terms positive set or null set for absolute measures. See the diagram below.

If we integrate the function $f$ over the interval $E_2$ using the Riemann integral, its value is certainly positive, but we do not call $E_2$ a positive set. In the example of the above figure, an interval that does not have any point where the function value is less than zero is a positive set. In the diagram, $E_{1}$, $E_{3}$ are positive sets, and $E_{5}$ is a negative set. $E_2$, $E_{4}$ are neither positive sets, negative sets, nor null sets. The most important point here is that a certain $E \in \mathcal{E}$ does not necessarily have to be a positive or negative set.

Theorem

• (a) A measurable subset of a positive set is also a positive set.

• (b) The countable union of arbitrary positive sets is also a positive set.

Proof

(a)

It’s trivial by the definition of a positive set.

(b)

Let $P_{1},\ P_2,\ \cdots$ be a positive set. And let us define $Q_{n}$ as follows.

$$Q_{1}=P_{1},\quad Q_{n}=P_{n}-\left( \bigcup \nolimits_{j=1}^{n-1}P_{j} \right)\ \forall\ n>1$$

Then $Q_{n} \subset P_{n}$ and each of $Q_{n}$ is disjoint. Therefore, $Q_{n}$ is a positive set by (a). Also, the following equation holds.

$$\bigcup \nolimits_{1}^{\infty} P_{j}=\bigcup \nolimits_{1}^{\infty} Q_{j}$$

Now, let $E$ be any measurable subset of $\bigcup \nolimits _{1}^\infty P_{n}$.

$$E \in \left( \bigcup \nolimits _{1}^\infty Q_{n} \right)=\left( \bigcup \nolimits _{1}^\infty P_{n} \right)$$

Then, proving $\nu (E) \ge 0$ concludes the proof. By the definition of $E$, the following equation is established. $$E= \bigcup \limits_{j=1}^\infty \left( Q_{j} \cap E \right)$$ Since each $Q_{n}$ is disjoint, by the countable additivity of sign measures, the following holds.

$$\nu (E) = \nu \left(\bigcup \nolimits_{j=1}^\infty \left( Q_{j} \cap E \right) \right) =\sum \limits_{j=1}^\infty \nu \left( Q_{j} \cap E \right)$$

Since $Q_{n}$ is a positive set and $(Q_{j}\cap E ) \subset Q_{j}$, the right side of the equation must be at least $0$.

$$\nu (E) =\sum \limits_{j=1}^\infty \nu \left( Q_{j} \cap E \right) \ge 0$$

■