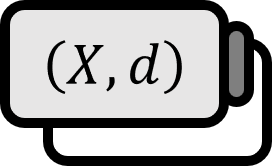Definition of a Metric Space
Definition
A function $d : X \times X \to [0, \infty)$ on a set set $X$ is called a distance and $\left( X, d\right)$ is called a metric space if it satisfies the following conditions with respect to $x,y,z \in X$. If the distance is trivial, the metric space is also simply denoted by $X$.
$d(x,y)=0 \iff x = y$
$d(x,y) = d(y,x)$
$d(x,y) + d(y,z) \ge d(x,z)$
Explanation
As one might know from the concept of norms in linear algebra, the size or distance does not necessarily have to be defined intuitively. The three examples below are defined specifically on $\mathbb{R}^{n}$, and as mentioned, are not much different from the norms seen in linear algebra. This is because a distance $d ( \mathbf{x} , \mathbf{y} ) := \left\| \mathbf{x} - \mathbf{y} \right\|$ can always be defined regardless of how a norm $\left\| \cdot \right\|$ is defined, therefore, if there is any kind of norm, there necessarily exists a corresponding distance.
Examples
Let’s consider $\mathbf{x} = (x_{1} , x_{2} , \cdots , x_{n} )$ and $\mathbf{y} = (y_{1} , y_{2} , \cdots , y_{n} ) $.
Euclidean distance: $d(\mathbf{x} , \mathbf{y}) = \sqrt{ \sum \limits_{i = 1}^{n} (x_{i} - y_{i} )^2 }$
Taxicab distance: $d^{\prime}(\mathbf{x} , \mathbf{y}) = \sum \limits_{i = 1}^{n} | x_{i} - y_{i} |$
Maximum distance: $d^{\prime \prime}(\mathbf{x} , \mathbf{y}) = \max \left\{ | x_{i} - y_{i} | \right\}_{i=1}^{n}$
In basic analysis, $\mathbb{R}^{1}$ is mainly dealt with, and it is safe to say that the Euclidean distance is mostly used. Specifically for analysis, there might not be a need to study metric spaces in detail, and it’s sufficient to accept the real number set $\mathbb{R}$ as a metric space $\left( \mathbb{R} , d \right)$. The two examples below are concepts of distance beyond Euclidean spaces.
Discrete distance:
$$ d_{0} (x,y) = \delta_{xy} = \begin{cases}1, & \ x \ne y \\ 0, & \ x = y \end{cases} $$
The discrete distance uses the Kronecker delta, which only considers whether two elements are the same. That it satisfies the triangle inequality can be easily proven by dividing into cases.
Integral distance:
$$ \rho (f,g) = \int_{a}^{b} | f(x) - g(x) | dx $$
The integral distance is a distance that can be defined in a set of continuous functions $C[a,b]$. If the graphs of two functions are completely the same, then the value is $0$.

The enclosed area by the solid line in the illustration represents $\rho (f,g)$.
From these definitions, it can be understood that metric is more appropriately understood as a ‘disparity’ rather than the traditional sense of ‘distance’. Since everything identical necessarily is $0$, what matters isn’t ‘how close to infinity’ but ‘how far from $0$’. For more abstract thinking, let’s move away from the intuitive notion that a larger distance means ‘farther away’ in terms of ’location’.