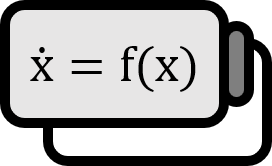📂Dynamics

Lyapunov Spectrum of Linear Systems

Theorem

For the matrix $A \in \mathbb{R}^{n \times n}$, let’s assume the following vector field is given as a linear differential equation. $$ \dot{\mathbf{x}} = A \mathbf{x} \qquad , \mathbf{x} \in \mathbb{R}^{n} $$

If $A$ is a symmetric matrix, the Lyapunov spectrum of this system is equal to the eigenvalues of ${\frac{ 1 }{ 2 }} \left( A + A^{T} \right)$.

---

• Here, $A^{T}$ is the transpose matrix of matrix $A$.

Explanation

$$ A = \begin{bmatrix} -0.2 & -0.3 \\ -0.2 & -0.7 \end{bmatrix} $$

julia> A = [-.2 -.3; -.3 -.7]
2×2 Matrix{Float64}:
 -0.2  -0.3
 -0.3  -0.7

julia> @showprogress for t in 0:h:tend
           # v, _ = RK4(T_A, v_[end])
           # push!(v_, v)

           U, V = gram_schmidt(U)
           λ += V |> eachcol .|> norm .|> log
           isinteger(t) && push!(λ_, λ / t)
           U = RK4(A, U, h)
       end
Progress: 100%|█████████████████████| Time: 0:00:05

As a concrete example, let’s calculate the Lyapunov spectrum for a linear system given by a matrix like $A = A^{T}$ mentioned above.

julia> λ / (tend)
2-element Vector{Float64}:
 -0.05958668545713238
 -0.8404133145577668

julia> eigen((A + A')/2).values
2-element Vector{Float64}:
 -0.8405124837953326
 -0.0594875162046673

Comparing the results of numerical calculations, we can confirm that they are quite similar to the theoretical predictions.

The point of calculating the Lyapunov spectrum for a simple system like this lies in the validation of the code. Unlike complex systems, linear systems allow for theoretical calculation of the Lyapunov spectrum, making it an example for verifying the accuracy of methods like RK4 and Gram-Schmidt orthogonalization or QR decomposition and their order.

Proof ¹

Definition of Lyapunov Spectrum:

Variational Equation: Let the following be the variational equation for the Jacobian matrix $J$ of $f$. $$ \dot{Y} = J Y $$ Here, the initial condition of the matrix function $Y = Y(t) \in \mathbb{R}^{n \times n}$ is set to be the identity matrix $Y(0) = I$. … Geometrically, you can think of $Y$ as showing how the tangent vector itself acts while transforming the original system slightly from $x(t)$ to $x(0)$.

$$ \lambda_{k} := \lim_{t \to \infty} \log \left[ \left( {\frac{ \left\| Y(t, v) v \right\| }{ \left\| v \right\| }} \right)^{1/t} \right] $$ The $\left\{ \lambda_{1} , \cdots , \lambda_{n} \right\}$ defined as above is called the Lyapunov spectrum or, $$ \Lambda_{v} := \lim_{t \to \infty} \left[ Y(t)^{\ast} Y(t) \right]^{1/2t} $$ The eigenvalues $\mu_{1} , \cdots , \mu_{n}$ of the matrix $\Lambda_{v}$ defined as above, when taking the logarithm of $\lambda_{k} := \log \mu_{k}$, is called the Lyapunov spectrum.

$\dot{\mathbf{x}} = A \mathbf{x}$ is a linear differential equation, so the Jacobian $J$ also becomes $J = A$ and the variational equation of the original system, for the initial value $Y = I_{n}$ which is the identity matrix, is $\dot{Y} = A Y$ and its exact solution is $Y(t) = e^{A t}$. According to the definition of the Lyapunov spectrum, the following is obtained. $$ \begin{align*} & \log \lim_{t \to \infty} \left[ Y(t)^{T} Y(t) \right]^{1/2t} \\ =& \lim_{t \to \infty} \log \left[ Y(t)^{T} Y(t) \right]^{1/2t} \\ =& \lim_{t \to \infty} {\frac{ 1 }{ 2t }} \log \left[ Y(t)^{T} Y(t) \right] \\ =& \lim_{t \to \infty} {\frac{ 1 }{ 2t }} \log \left[ e^{A^{T} t} e^{A t} \right] \end{align*} $$

🔒(25/12/30)Matrix Exponential and Matrix Logarithm: If two matrices $A, B \in \mathbb{C}^{n \times n}$ satisfy $AB = BA$, the following holds. $$ \log AB = \log A + \log B - 2 \pi i \mathcal{U} \left( \log A + \log B \right) $$ Especially, for the eigenvalues of $A$ $\mu_{k}$ and those of $B$ $\nu_{k}$, the following corollary can be obtained. $$ \log AB = \log A + \log B \iff \forall k = 1 , \cdots , n : \arg \mu_{k} + \arg \nu_{k} \in ( - \pi , \pi ] $$

Since $A \in \mathbb{R}^{n \times n}$ has only real entries, it is an Hermitian matrix, and its eigenvalues are real, the eigenvalues of both $e^{A^{T} t}$ and $e^{A t}$ are real. Having real eigenvalues means their arguments are $0$, ensuring the matrix logarithm $\log A B = \log A + \log B$ is valid, leading to the following. $$ \begin{align*} & \lim_{t \to \infty} {\frac{ 1 }{ 2t }} \log \left[ e^{A^{T} t} e^{A t} \right] \\ =& \lim_{t \to \infty} {\frac{ 1 }{ 2t }} \left[ \log e^{A^{T} t} + \log e^{A t} \right] \\ =& \lim_{t \to \infty} {\frac{ 1 }{ 2t }} \left[ A^{T} t + A t \right] \\ =& {\frac{ 1 }{ 2 }} \left[ A^{T} + A \right] \end{align*} $$

■

Code

The following is a result of calculating the Lyapunov spectrum using Julia.

using ProgressMeter, LinearAlgebra

function gram_schmidt(J)
    N = size(J, 1)
    U, V = deepcopy(J), deepcopy(J)
    U[:,1] = V[:,1] / norm(V[:,1])
    for j in 2:N
        for jp in 1:(j-1)
            V[:,j] -= (J[:,j]'U[:,jp])*U[:,jp]
        end
        U[:,j] = V[:,j] / norm(V[:,j])
    end
    return U, V
end
function RK4(J::AbstractMatrix, U::AbstractMatrix, dt=1e-2)
    V1 = J*U
    V2 = J*(U + (dt/2)*V1)
    V3 = J*(U + (dt/2)*V2)
    V4 = J*(U + dt*V3)
    return U + (dt/6)*(V1 + 2V2 + 2V3 + V4)
end

A = [-.2 -.3; -.3 -.7]
# T_A(v) = A*v

U = I(2)
λ = zeros(2); λ_ = [λ]
# v = [10, 10.0]; v_ = [v]
h = 1e-3; tend = 1000
@showprogress for t in 0:h:tend
    # v, _ = RK4(T_A, v_[end])
    # push!(v_, v)

    U, V = gram_schmidt(U)
    λ += V |> eachcol .|> norm .|> log
    isinteger(t) && push!(λ_, λ / t)
    U = RK4(A, U, h)
end
λ / (tend)
eigen((A + A')/2).values

using Plots
plot(xlims = [1, 100], xlabel = "t", legend = :right)
scatter!(0:10:1001, first.(λ_[1:10:end]), label = "λ1", msw = 0)
scatter!(0:10:1001,  last.(λ_[1:10:end]), label = "λ2", msw = 0)
hline!(eigen((A + A')/2).values, color = :black, label = "Theoretical")