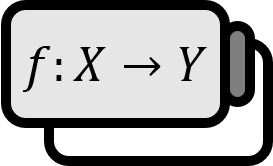Diagonal Matrix as a Function, Diagonal Elements
Definition
Diagonal Elements
The $\text{diag} : \mathbb{R}^{n \times n} \to \mathbb{R}^{n}$ for a matrix is defined as the vector consisting of the diagonal elements of the matrix.
$$ \text{diag} A = \begin{bmatrix} A_{11} \\ A_{22} \\ \vdots \\ A_{nn} \end{bmatrix} $$
Diagonal Matrix
The $\text{diag} : \mathbb{R}^{n} \to \mathbb{R}^{n \times n}$ for a vector is defined as the matrix that has the vector as its diagonal elements. $$ \text{diag} \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{bmatrix} = \begin{bmatrix} x_{1} & 0 & \cdots & 0 \\ 0 & x_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & x_{n} \end{bmatrix} $$
Explanation
The $\text{diag}$ related to diagonal matrices can be defined in two ways when viewed as a function. There might be cases where the exact same notation is used differently in literature, but since the dimensions can be calculated, there’s no need to worry about getting confused.
In Programming Languages
The following is MATLAB code, where both functions are overloaded so they can be cleverly used whether the argument is a matrix or a vector. If a matrix is input, it returns the diagonal elements, and if a vector is input, it returns a diagonal matrix.
>> X
X =
1 4 7
2 5 8
3 6 9
>> diag(X)
ans =
1
5
9
>> Y
Y =
3
2
1
>> diag(Y)
ans =
3 0 0
0 2 0
0 0 1
On the other hand, in Julia, it is separated into two functions.
julia> A = [
1 0 3
0 5 1
3 1 9
]
3×3 Matrix{Int64}:
1 0 3
0 5 1
3 1 9
julia> diag(A)
3-element Vector{Int64}:
1
5
9
julia> diagm([1,5,9])
3×3 Matrix{Int64}:
1 0 0
0 5 0
0 0 9