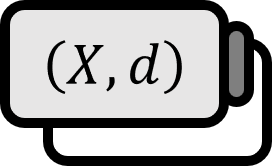The inverse of a continuous bijection on a compact metric space is continuous.
Theorem
Let $X$ be a compact metric space, and let $Y$ be a metric space. Assume that $f : X \to Y$ is a bijective continuous function. Then, the inverse $f^{-1}$ of $f$, defined as follows, is bijective and continuous.
$$ f^{-1} (f(x))=x, \quad x\in X $$
The compactness condition is essential
Proof
Equivalent conditions for continuity in metric spaces
For two metric spaces $(X,d_{X})$ and $(Y,d_{Y})$, let $f : X \to Y$. Then, the following two propositions are equivalent:
$f$ is continuous in $X$.
For every open set $O_{Y}$ of $Y$, $f^{-1}(O_{Y})$ is an open set in $X$.
Applying the equivalence condition for continuity in metric spaces in reverse to $f^{-1}$, the continuity of $f^{-1}$ is equivalent to, for every open set $O_{X}$ of $X$, $f(O_{X})$ being an open set in $Y$. Therefore, the proof unfolds in this direction. First, select an arbitrary open set $O_{X}$ in $X$. Then, $(O_{X})^{c}=C_{X}$ is a closed set in $X$. Since the closed subset of a compact set is compact, $C_{X}$ is compact.
Let $X$ be a compact metric space, and $Y$ a metric space, and suppose $f:X\to Y$ is continuous. Then, $f(X)$ is compact.
Thus, by the lemma, $f(C_{X})$ is compact. Since a compact subset in a metric space is a closed set, $f(C_{X})$ is closed. Assuming that $f$ is bijective, $(f(C_{X}))^{c}=f((C_{X})^{c})=f(O_{X})$ and therefore $f(O_{X})$ is an open set as it is the complement of a closed set.
■